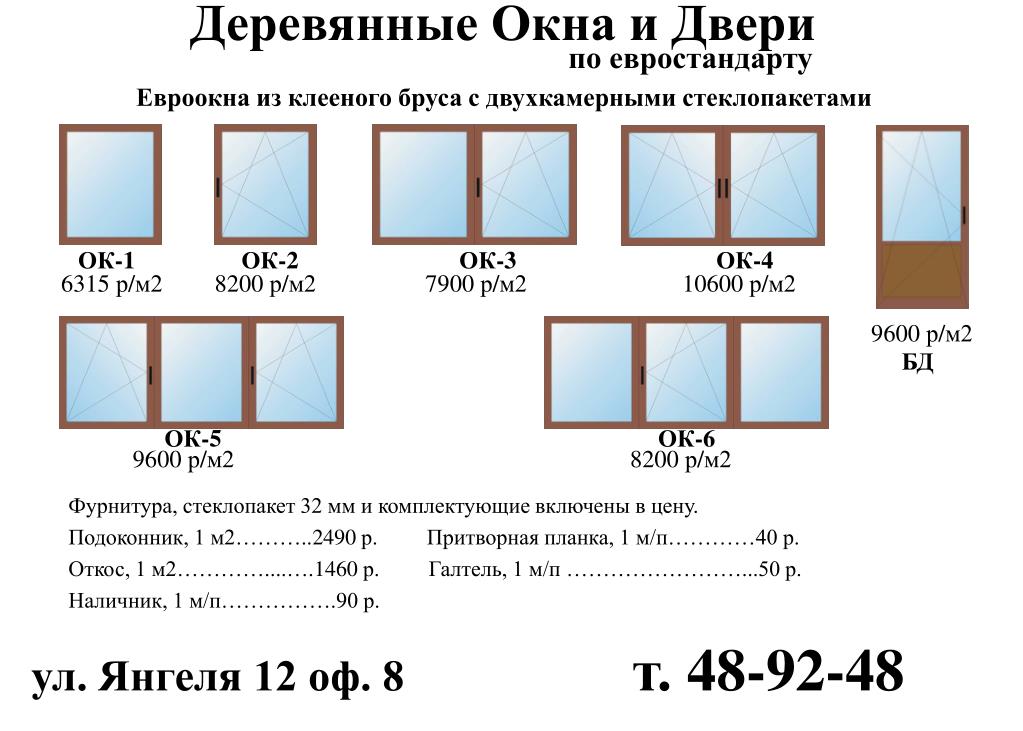
Какова общая площадь окон: 1)Какова площадь вашего дома? Сколько человек будет жить в нём? 2)Где будет расположен дом? Как он ориентирован относительно сторон света? Какие особенности рельефа, климата и др. надо учесть? 3)Из каких материалов будет построен дом? Какова общая площадь окон? 4)Каков источник водоснабжения? 5)Как утилизируются отходы и мусор, как устроена канализация? 6)Каким образом дом отапливается? 7)Как дом освещается, какие бытовые электроприборы используются?
Размеры частного дома
Вопросы, рассмотренные в материале:
- С чего начинаются расчеты размеров частного дома
- Оптимальные размеры дома: сколько нужно комнат
- Приблизительные размеры комнат в частном доме
- Рекомендуемые размеры окон в частном доме
- Размер дверей в частном доме
Размеры частного дома зависят от множества факторов. Начиная от самых простых и очевидных – бюджета строительства, заканчивая количеством проживающих, преобладающей погодой в регионе, назначением и желаемым количеством помещений.
Помимо общей площади, важно уделить внимание правильному подбору размера комнат в доме, окон и дверей. От этих факторов напрямую будет зависеть комфорт жильцов. Как рассчитать все эти параметры и что еще нужно учесть при выборе размеров частного дома, читайте в нашем материале.
С чего начинаются расчеты размеров частного дома
Собираясь строить собственный дом, в первую очередь думают о его площади и размерах. Задача эта не из простых, особенно если сталкиваетесь с ней впервые. Мало принять решение о количестве комнат и этажности здания, нужно еще определиться с размерами помещений.
Задача эта не из простых, особенно если сталкиваетесь с ней впервые. Мало принять решение о количестве комнат и этажности здания, нужно еще определиться с размерами помещений.
Нередки крайности от застройщиков во время планировочных работ по частному дому:
- Долгая жизнь в тесной квартире провоцирует желание большого пространства. И вот во что это выливается при проектировании дома: хочется побольше комнат, а площадь помещений тоже максимизировать. Однако практика показывает, что желания часто превышают необходимость.
- Совершенно противоположный подход – экономия места во всем, в том числе в количестве комнат и их размерах.
Оба вышеперечисленных подхода негативно сказываются на результате. Нерациональное увеличение размеров частного дома приводит к существованию незадействованных комнат и пустующему пространству в них. Это неиспользуемое место придется отапливать, убирать, каким-то образом обустроить. А самое главное, что существенно вырастет стоимость строительства.
Тотальная экономия приведет к сооружению дома и маленького, и тесного. Очень быстро потенциал такого здания будет исчерпан, место станет дефицитным. Придется достраивать комнаты или сооружать отдельную хозпостройку для складирования различных инструментов, инвентаря и других незаменимых в хозяйстве предметов.
Чтобы не впасть в крайности, нужно определиться с оптимальным размером будущего жилища. На первый план выходят не общие квадратные метры, а число отдельных комнат, их размещение и площадь.
Показателен в этом отношении пример с количеством спален. В одном доме площадью 150 кв. м. множество спален, поэтому на гостиную и кухню осталось меньше места. При этом некоторые спальни используются крайне редко. Получается, что основная жилая площадь для семьи не более 100 кв. м. Другой дом имеет общую площадь 120 кв. м., большую кухню и гостиную. Спален ровно столько, сколько необходимо домочадцам. В итоге вся площадь дома используется оптимально.
Несмотря на грубость примера, он достаточно хорошо иллюстрирует необходимость тщательного продумывания планировки дома, его размеров, площади отдельных помещений.
Оптимальные размеры дома: сколько нужно комнат
Стандартные размеры частного дома предполагают количество комнат, равное числу жильцов плюс один. Данным эталоном разумно руководствоваться, адаптировав под свою семью. Например, дети, пока маленькие, могут проживать в одном помещении. Однако по мере взросления каждому ребенку лучше выделить отдельную комнату.
В случае частых визитов родни и друзей неплохо продумать места для их размещения. Предусмотреть нужно и дополнительные комнаты, такие как сауна, игровая для детей, спортзал и, возможно, терраса. Если дом многоэтажный, на каждом из этажей требуется обязательно оборудовать санузел.
При проектировании собственного дома не помешает постараться спрогнозировать будущее своей семьи на 10–15 лет вперед. Планируется ли совместное проживание с родителями или детьми? Будут ли рождаться новые члены семейства? А может, кто-то из родственников хочет переехать к вам?
Приблизительные размеры комнат в частном доме
В недалеком прошлом, даже еще пару лет назад считалось, для семьи из 3-4 человек для комфортного проживания нужен особняк площадью не менее 200–250 м2. Сейчас в сфере загородного строительства доминируют совсем другие тенденции. Акцент внимания сместился в сторону энергоэффективности зданий, достижения рационального баланса между комфортом и оптимизацией площади.
Сейчас в сфере загородного строительства доминируют совсем другие тенденции. Акцент внимания сместился в сторону энергоэффективности зданий, достижения рационального баланса между комфортом и оптимизацией площади.
Современность диктует совсем другие нормы размеров частного дома. Для подавляющего большинства семей из 3-4 человек (супруги и дети) оказалось достаточно иметь 120–150 м2 площади. В эту цифру не входят размеры гаража. Каким образом была получена площадь оптимального современного жилого строения?
Параметры собственного жилища – не только вопрос желания и возможностей. Существуют стандартные размеры частного дома, придерживаться которых нужно обязательно. Например, площадь ванной нельзя сокращать меньше 3,3 м2, туалет должен быть хотя бы 1,5 м2. Если санузел планируется совмещенный, его площадь должна составлять от 3,8 м2. Так как строительство загородного дома само собой предполагает желание владельцев получить дополнительный комфорт, поэтому наиболее оптимальными параметрами являются следующие:
- прихожая – 4–8 м2;
- гостиная – 25–30 м2;
- спальня для взрослых – 16–20 м2;
- комната для каждого ребенка – 14–18 м2;
- столовая с кухней – 16–20 м2;
- гардеробная – 4–6 м2;
- ванная комната – 4–8 м2;
- вспомогательные комнаты (прачечная, кладовая, бойлерная, котельная и т.
 д.) – 4–6 м2.
д.) – 4–6 м2.
Часть полезной площади здания может быть занято коридорами. Поэтому нужно постараться максимально избавиться от них в ходе проектирования. В стандартные размеры частного дома заложено наличие санузла на каждом этаже. Если же площади достаточно и финансы не ограничены, тогда неплохо предусмотреть отдельные ванные комнаты для родителей, детей и гостей.
Если в доме есть цокольный этаж с размещенными там спортзалом или сауной, нелишним будет обустройство рядом еще одного санузла.
Проектируя частное жилище, нужно предусмотреть следующие элементы:
- Входной узел (тамбур) нужен для разграничения жилых помещений и улицы. Таким способом зимой отсекается холодный воздух с улицы, не допускается его попадание в жилой объем. Оставляя в тамбуре грязную обувь, можно также существенно снизить попадание грязи в жилые комнаты. Поэтому улицу и жилое пространство должно обязательно разделять две двери.
- Помещение под названием котельная, топочная или агрегатная.
 Жилище необходимо оснастить множеством инженерного оборудования: водяные очищающие фильтры, котлы, насосы. Чтобы разместить всю эту технику, к размерам частного дома нужно добавить отдельную комнату с оптимальной площадью – 4-5 м2.
Жилище необходимо оснастить множеством инженерного оборудования: водяные очищающие фильтры, котлы, насосы. Чтобы разместить всю эту технику, к размерам частного дома нужно добавить отдельную комнату с оптимальной площадью – 4-5 м2. - Лестницу на второй этаж. Этот элемент здания забирает довольно много свободного места – до 5-6 м2, даже если предусмотреть эффективное использование площади под лестницей (кладовая, шкаф, ящики).
Кроме того, популярностью в загородных домах пользуются кабинеты (площадь 12–14 м2), библиотеки (от 10 до 14 м2) и игровые помещения (16–18 м2). При желании иметь встроенный одноместный гараж нужно отдавать себе отчет, что он займет площадь от 20 до 25 м2, а если хочется разместить два автомобиля, помещение должно занимать уже 30–40 м2. Данная площадь предусматривает место для хранения сезонных шин, велосипедов и садового инструмента.
Размеры частного дома для проживания всего двух человек вполне вкладываются в рамки 100 кв. м.
м.
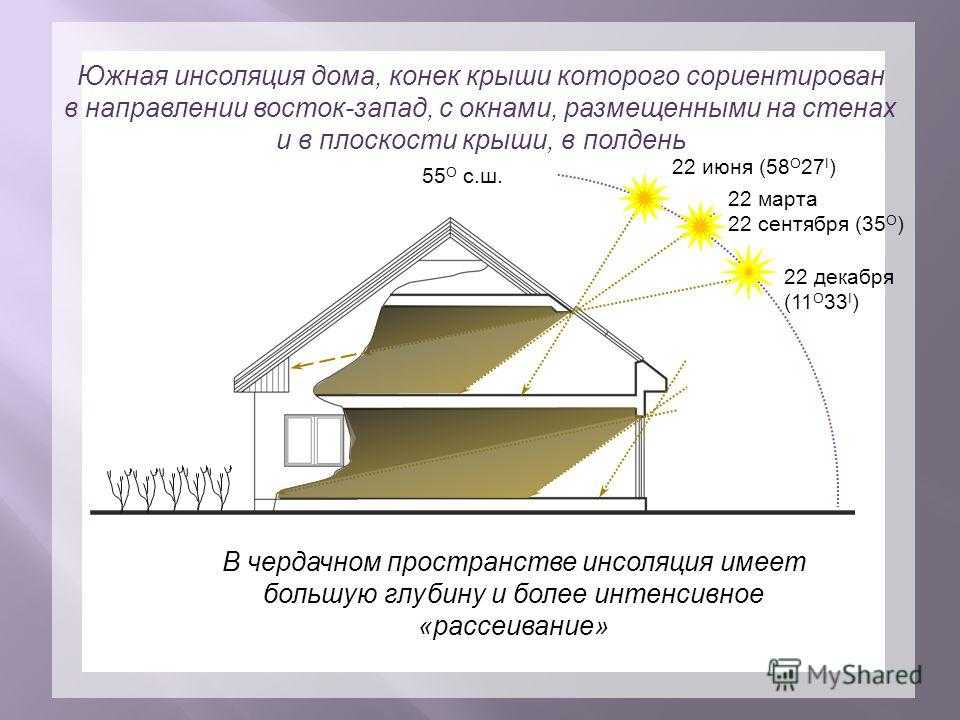
Рекомендуемые размеры окон в частном доме
Не существует стандартов, жестко регламентирующих площадь остекления в частном домостроении. Поэтому размер и количество окон остается на усмотрение застройщика. Компании по производству окон готовы выполнить заказ с любыми нестандартными параметрами. Однако стоит отдавать себе отчет, что отклонение от типовых размеров влечет удорожание производства, монтажа и последующего обслуживания окон.
Модное ныне панорамное остекление на большой площади требует в доме мощной отопительной установки. Кроме того, возрастают расходы на эксплуатацию и ремонт таких оконных конструкций. Стандартные размеры частного дома чаще всего предполагают обычные параметры окон. Тут следует ориентироваться на проемы, используемые в типовом многоэтажном строительстве.
Выбирая размер и расположение окон, нужно учитывать функционал комнаты, расположение сторон света и геометрию самого помещения. Именно по этой причине лучше придерживаться приведенной ниже пошаговой схемы:
- Площадь остекления рассчитывается путем деления квадратуры помещения на 6–
- Далее высота окна выбирается из стандартного ряда проемов гражданского строительства.

- Общая ширина окон получается делением площади остекления на высоту.
- Выбирается ширина проема из стандартного ряда.
- Количество окон рассчитывается делением общей ширины на ширину стандартного проема.
Рассчитанные таким способом параметры окон нуждаются в корректировке. Необходимо добавить 20 мм к ширине и 50 мм к высоте – эти зазоры нужны для монтажной пены, используемой при установке окон. Все дробные числа округляются в сторону увеличения. Метод позволяет получить в частном доме окна, наиболее приближенные к строительным нормативам.
Размер дверей в частном доме
Предпочтительнее также использовать стандартные двери. Это дешевле изготовления изделий по индивидуальным размерам, а их функционал и конструкция одинаковы. Стандартизированные двери проще и быстрее установить. Кроме того, вы получаете полностью соответствующее санитарным правилам и нормам изделие:
- Дверной проем высотой не менее 1,9 м.
- Ширина проема от 0,8 м, если жильцов более 15 человек – проем составляет от 1,2 м.

В правилах ничего не говорится о толщине, однако совершенно понятно, что ее должно быть достаточно для функционала входных дверей.
Также в нормативной документации не регламентируется сторона открывания двери. Однако в случае пожара гораздо более правильно, если они открываются наружу. Данный пункт нашел свое отражение в правилах пожарной безопасности.
ГОСТ в основном касается повсеместно распространенных и недорогих дверей с одной створкой. Однако многочисленные производители сегодня выпускают широкую линейку различных дверных изделий, соответствующим всем строительным нормам. Число вариаций отделки, возможности комплектации дверей сделали промышленные образцы не хуже, а может, даже лучше выполненных по индивидуальным заказам.
Считается, что частные дома не обязаны соответствовать СНиП. Но актуальные правила пожарной безопасности рассматривают все дверные проемы как эвакуационные выходы. Последние, в свою очередь, должны иметь геометрические размеры не меньше определенного минимума.
В погоне за индивидуальностью некоторые отходят от стандартных размеров частного дома и делают проемы необычными по размерам. Чтобы не противоречить правилам, проемы увеличивают по сравнению с типовыми. При использовании оригинальных, необычных конструкций параметры их могут быть определены только непосредственными измерениями на объекте.
Частный дом зачастую является местом воплощения дизайнерских идей его владельцев. Встречаются и совсем оригинальные строения, настоящие арт-объекты. Размеры дверей в таких частных домах могут быть также нестандартными и не отвечающими нормативам.
Все подобные изделия тоже можно разбить на категории:
- Полуторные. Означает присутствие двух полотен в коробке. Одно стандартизированной ширины, второе уменьшенное. Необходимость в таком решении возникает, если габариты дверного проема нестандартные. Малое полотно обычно редко используется и большую часть времени остается в закрытом состоянии.
- Двустворчатые.
 Дверной блок состоит из двух одинаковых полотен. В летний сезон открывают обе створки, зимой одну фиксируют и пользуются только второй.
Дверной блок состоит из двух одинаковых полотен. В летний сезон открывают обе створки, зимой одну фиксируют и пользуются только второй. - С фрамугой. Высота коробки таких дверей увеличена. Вне зависимости от количества полотен снизу сверху присутствует форточка или декоративный элемент. Решение подходит для специально спланированных для этого или нестандартных проемов. Благодаря необычности конструктивного решения фасад здания выглядит более индивидуально и эксклюзивно.
Какая бы конструкция дверей не применялась, важно помнить, что размер основного полотна, через которое в основном будет осуществляться проход, должен составлять 90 см. Именно такая ширина обеспечит удобство эксплуатации и безопасность в случае чрезвычайной ситуации.
Что же касается размеров частного дома, то лучше всего не поддаваться эмоциям и желанию превзойти всех соседей, показав богатство. Гораздо разумнее подойти к планировке собственного жилища из практических соображений.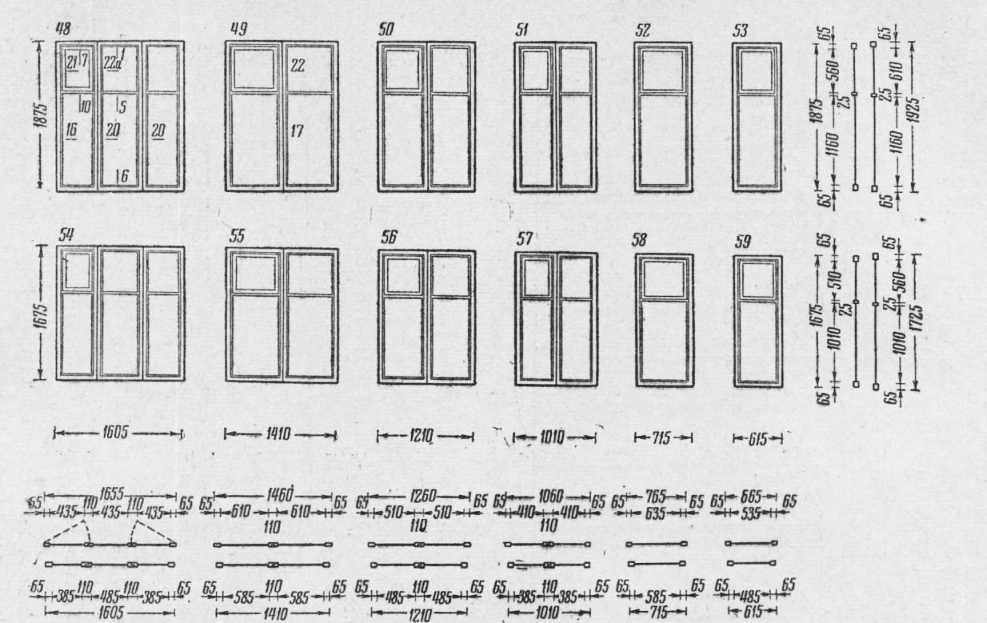 Немало примеров реальных семейных пар, которые вполне счастливы на 40 м2. Конечно же это возможно тогда, когда их дети уже выросли и разъехались по своим домам.
Немало примеров реальных семейных пар, которые вполне счастливы на 40 м2. Конечно же это возможно тогда, когда их дети уже выросли и разъехались по своим домам.
Как посчитать площадь комнаты, стены, пола, потолка
Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.
Часто требуется посчитать кубатуру комнаты, ее объем
Содержание статьи
- 1 Площадь комнаты в квадратных метрах
- 1.1 Прямоугольная комната
- 1.2 Помещение неправильной формы
- 2 Как рассчитать квадратуру стен
- 3 Объем комнаты
Площадь комнаты в квадратных метрах
Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:
Для этого нужны будут:
- Рулетка. Лучше — с фиксатором, но подойдет и обычная.
- Бумага и карандаш или ручка.
- Калькулятор (или считайте в столбик или в уме).
Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.
Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.
Прямоугольная комната
Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).
Как высчитать площадь комнаты
Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.
Помещение неправильной формы
Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).
Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.
Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.
Площадь комнаты сложной формы
Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):
- Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв.
 м.
м. - Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
- Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.
Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.
Как посчитать площадь комнаты неправильной формы
В этом случае порядок вычислений такой:
- Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
- Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
- Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв.
 м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м. - Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.
Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.
Формулы расчета площади и периметра простых геометрических фигур
Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.
Как рассчитать квадратуру стен
Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:
- высота потолков;
- высота и ширина дверных проемов;
- высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.
Удобнее всего размеры наносить на план
Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.
- Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
- Стена с окном:
- квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
- сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
- стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.
Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.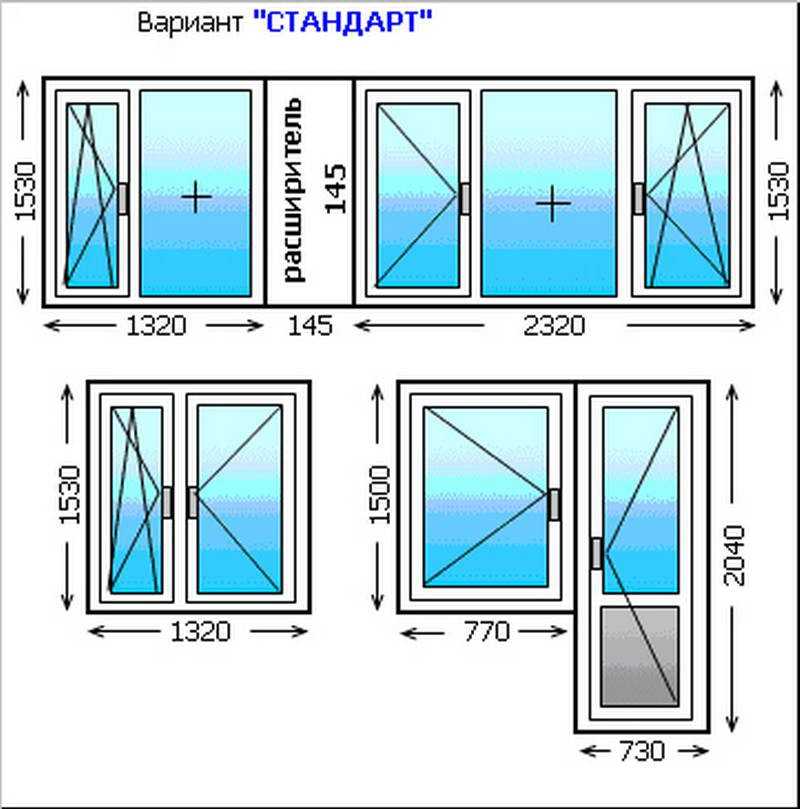 м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.
Объем комнаты
Формула расчета объема комнаты
Для некоторых расчетов требуется объем комнаты. В этом случае перемножаются три величины: ширина, длинна и высота помещения. Измеряется данная величина в кубических метрах (кубометрах), называется еще кубатурой. Для примера используем данные из предыдущего пункта:
- длинна — 5,6 м;
- ширина — 3,2 м;
- высота — 2,5 м.
Если все перемножить, получаем: 5,6 м * 3,2 м * 2,5 м = 44,8 м3. Итак, объем помещения 44,8 куба.
Вычисление площади | SkillsYouNeed
Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.
На этой странице собрана основная информация, которую вам необходимо знать, чтобы понимать и вычислять площади обычных фигур, включая квадраты и прямоугольники, треугольники и круги.
Расчет площади методом сетки
Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.
В этом примере внутри прямоугольника 10 квадратов сетки.
Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.
В этом примере используются сантиметры, но тот же метод применим для любой единицы длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. д.
В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному «квадратному сантиметру».
Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.
Имеется 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.
В математике квадратные сантиметры сокращаются до см 2 . 2 означает «квадратный».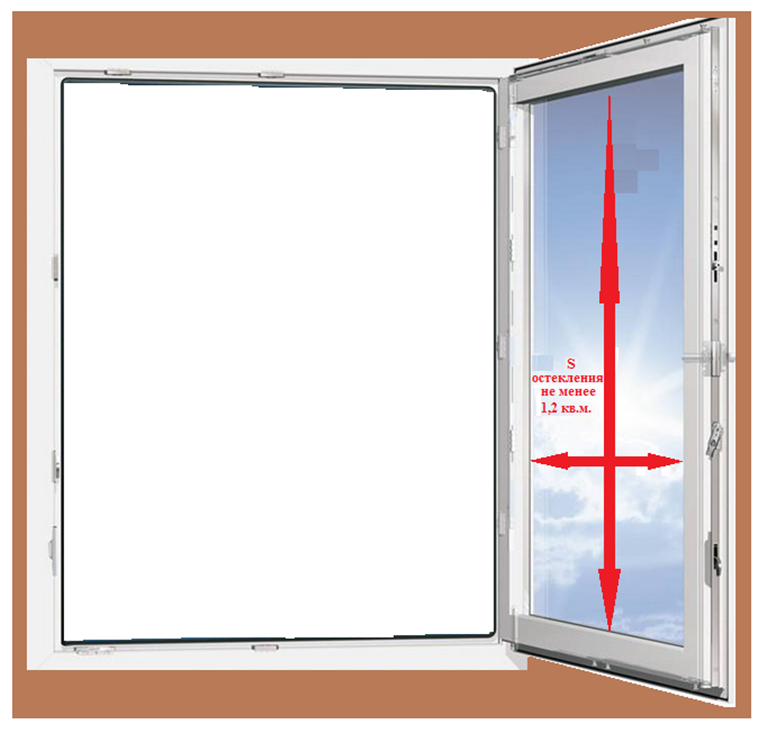
Каждый квадрат сетки равен 1 см 2 .
Площадь большого квадрата 16см 2 .
Подсчет квадратов на сетке для нахождения площади работает для всех фигур, если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.
В этом примере квадрат не вписывается точно в сетку.
Мы все еще можем вычислить площадь, считая квадраты сетки.
- Имеется 25 полных квадратов сетки (заштрихованы синим цветом).
- 10 половинных квадратов сетки (заштрихованы желтым цветом) – 10 половинных квадратов соответствуют 5 полным квадратам.
- Также есть 1 четверть квадрата (заштриховано зеленым цветом) – (¼ или 0,25 целого квадрата).
- Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.
Следовательно, площадь этого квадрата равна 30,25 см 2 .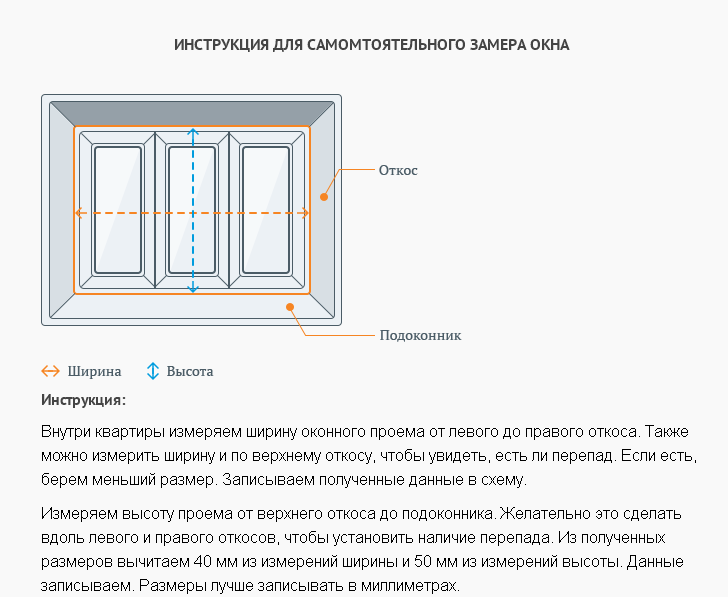
Вы также можете записать это как 30¼cm 2 .
Хотя использование сетки и подсчет квадратов внутри формы является очень простым способом изучения понятий площади, он менее полезен для нахождения точных площадей с более сложными формами, когда может быть много долей квадратов сетки, которые нужно сложить вместе.
Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.
Оставшаяся часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сетки.
Площади простых четырехугольников:
Квадраты, прямоугольники и параллелограммы
Простейшие (и наиболее часто используемые) вычисления площадей предназначены для квадратов и прямоугольников.
Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.
Площадь прямоугольника = высота × ширина
Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это само на себя, чтобы найти площадь. Это то же самое, что сказать длину 2 или длина в квадрате.
Это то же самое, что сказать длину 2 или длина в квадрате.
Хорошей практикой является проверка того, что фигура на самом деле является квадратом, путем измерения двух сторон. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измерите, вы обнаружите, что на самом деле это прямоугольник.
Часто в реальной жизни формы могут быть более сложными. Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.
Типовой план помещения не может состоять из простого прямоугольника или квадрата:
В этом и других подобных примерах хитрость заключается в том, чтобы разбить фигуру на несколько прямоугольников (или квадратов). Неважно, как вы разделите фигуру — любое из трех решений приведет к одному и тому же ответу.
Решение 1 и 2 требуют, чтобы вы сделали две фигуры и сложили их площади вместе, чтобы найти общую площадь.
Для решения 3 вы делаете большую фигуру (A) и вычитаете из нее меньшую фигуру (B), чтобы найти площадь.
Другая распространенная проблема заключается в том, чтобы найти область границы — фигура внутри другой фигуры.
В этом примере показан путь вокруг поля шириной 2 метра.
Опять же, в этом примере есть несколько способов определить площадь пути.
Вы можете рассматривать путь как четыре отдельных прямоугольника, вычислять их размеры, затем их площадь и, наконец, складывать площади вместе, чтобы получить общую сумму.
Более быстрым способом было бы определить площадь всей фигуры и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из целого, оставив площадь пути.
- Площадь всей фигуры 16 м × 10 м = 160 м 2 .
- Мы можем рассчитать размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 м.
- Ширина всей фигуры 16 м, а ширина пути по всей фигуре 4 м (2 м слева от фигуры и 2 м справа). 16м — 4м = 12м
- То же самое можно сделать для высоты: 10 м — 2 м — 2 м = 6 м
- Итак, мы подсчитали, что средний прямоугольник имеет размеры 12 м × 6 м.

- Таким образом, площадь среднего прямоугольника равна: 12 м × 6 м = 72 м 2 .
- Наконец, мы отделяем площадь среднего прямоугольника от площади всей фигуры. 160 — 72 = 88м 2 .
Площадь пути 88 м 2 .
A Параллелограмм — это четырехсторонняя фигура с двумя парами сторон одинаковой длины — по определению прямоугольник — это разновидность параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.
Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что под высотой понимается не длина вертикальных (или не вертикальных) сторон, а расстояние между сторонами .
Из диаграммы видно, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.
Представьте воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.
Это высота.
Вычисление площади треугольников
Треугольник можно представить как половину квадрата или параллелограмма.
Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь, используя следующую формулу:
Площадь треугольника = (высота × ширина) ÷ 2.
Другими словами, вы можете вычислите площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите ответ на 2.
Высота треугольника измеряется как прямоугольная линия от нижней линии (основания) до «вершины» (верхней точки) треугольника.
Вот несколько примеров:
Площадь трех треугольников на диаграмме выше одинакова.
Каждый треугольник имеет ширину и высоту 3 см.
Площадь вычисляется:
(высота × ширина) ÷ 2
3 × 3 = 9
9 ÷ 2 = 4,5
Площадь каждого треугольника равна 4,5 см 2 .
В реальных ситуациях вы можете столкнуться с задачей, требующей нахождения площади треугольника, например:
Вы хотите покрасить фронтон сарая.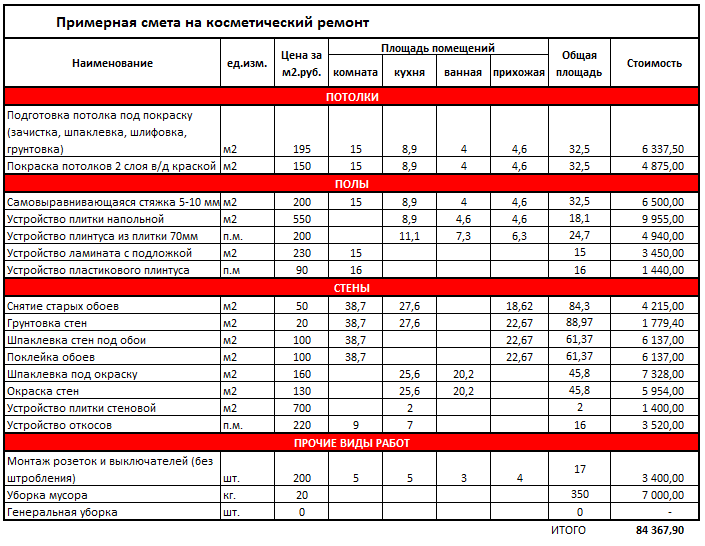 Вы только хотите посетить отделочный магазин один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10м 2 стены. Сколько краски нужно, чтобы покрыть фронтон?
Вы только хотите посетить отделочный магазин один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10м 2 стены. Сколько краски нужно, чтобы покрыть фронтон?
Вам нужно три измерения:
A — Общая высота до вершины крыши.
B — Высота вертикальных стен.
C — Ширина здания.
В этом примере размеры:
A — 12,4 м
B — 6,6 м
C — 11,6 м
Следующий этап требует дополнительных расчетов. Думайте о здании как о двух формах, прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительные измерения, необходимые для определения площади конца фронтона.
Размер D = 12,4 – 6,6
D = 5,8 м
Теперь можно вычислить площадь двух частей стены:
Площадь прямоугольной части стены: 6,6 × 11,6 = 76,56 м 2
Площадь треугольной части стены: (5,8 × 11,6) ÷ 2 = 33,64 м 2
Сложите эти две площади вместе, чтобы найти общую площадь:
76,56 + 33,64 м = 1100
Как известно, один литр краски покрывает 10 м 2 стены, чтобы мы могли вычислить, сколько литров нам нужно купить:
110,2 ÷ 10 = 11,02 литра.
На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых банках, в результате получается чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!
Площади кругов
Для вычисления площади круга необходимо знать его диаметр или радиус .
Диаметр окружности — это длина прямой линии от одной стороны окружности до другой, проходящей через центральную точку окружности. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)
Радиус окружности — это длина прямой линии от центральной точки окружности до ее края.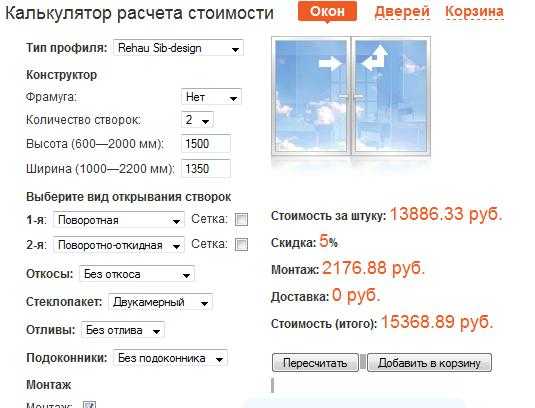 Радиус равен половине диаметра. (радиус = диаметр ÷ 2)
Радиус равен половине диаметра. (радиус = диаметр ÷ 2)
Вы можете измерить диаметр или радиус в любой точке окружности – важно измерять с помощью прямой линии, которая проходит через (диаметр) или заканчивается (радиус) в центре окружности.
На практике при измерении окружностей часто бывает проще измерить диаметр, чем разделить его на 2, чтобы найти радиус.
Радиус нужен для вычисления площади круга, формула такова:
Площадь круга = πR 2 .
Это означает:
π = Pi — константа, равная 3,142.
R = радиус окружности.
R 2 (радиус в квадрате) означает радиус × радиус.
Следовательно, круг с радиусом 5 см имеет площадь:
3,142 × 5 × 5 = 78,55 см 2 .
Круг диаметром 3м имеет площадь:
Сначала вычисляем радиус (3м ÷ 2 = 1,5м)
Затем применяем формулу:
πR 2
3,142 × 1,5 × 1,5 = 7,0695.
Площадь круга диаметром 3 м равна 7,0695 м 2 .
Заключительный пример
Этот пример использует большую часть содержимого этой страницы для решения простых задач с площадями.
Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (регистрационный номер: 376599).
Этот пример включает в себя нахождение площади фасада дома, деревянной решетчатой части, исключая дверь и окна. Вам нужны следующие мерки:
| А – 9,7 м | В – 7,6 м |
| С – 8,8 м | Г – 4,5 м |
| В – 2,3 м | В – 2,7 м |
| Г – 1,2 м | В – 1,0 м |
Примечания:
- Все измерения являются приблизительными.
- О бордюре вокруг дома можно не беспокоиться – он не учитывался при измерениях.
- Мы предполагаем, что все прямоугольные окна имеют одинаковый размер.

- Размер круглого окна — это диаметр окна.
- Размеры двери включают ступени.
Какова площадь деревянной решетчатой части дома?
Вычисления и ответы ниже:
Ответы на приведенный выше пример
Сначала вычислите площадь основной формы дома – прямоугольника и треугольника, составляющих фигуру.
Основной прямоугольник (В × С) 7,6 × 8,8 = 66,88м 2 .
Высота треугольника (A – B) 9,7 – 7,6 = 2,1.
Следовательно, площадь треугольника равна (2,1 × C) ÷ 2,
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м 2 .
Суммарная полная площадь фасада дома равна сумме площадей прямоугольника и треугольника:
66,88 + 9,24 = 76,12 м 2 .
Затем определите площади окон и дверей, чтобы их можно было вычесть из общей площади.
Площадь двери и ступеней составляет (D × E) 4,5 × 2,3 = 10,35 м 2 .
Площадь одного прямоугольного окна составляет (G × F) 1,2 × 2,7 = 3,24 м 2 .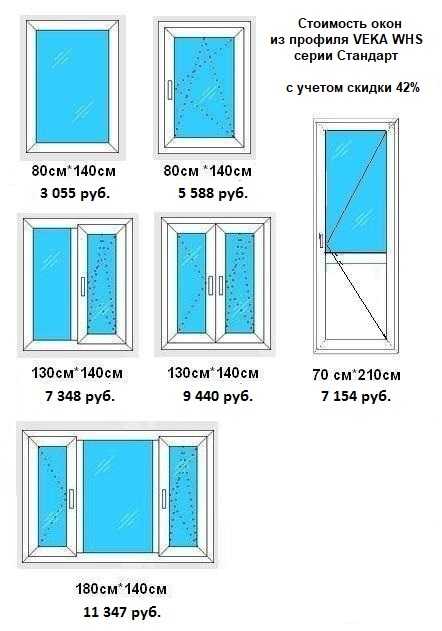
Пять прямоугольных окон. Умножьте площадь одного окна на 5.
3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).
Круглое окно имеет диаметр 1 м, поэтому его радиус равен 0,5 м.
Используя πR 2 , определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855 м 2 .
Затем добавьте площади дверей и окон.
(площадь дверей) 10,35 + (площадь прямоугольных окон) 16,2 + (площадь круглых окон) 0,7855 = 27,3355
Наконец, вычтите общую площадь окон и дверей из полной площади.
76,12 – 27,3355 = 48,7845
Площадь деревянного реечного фасада дома, а ответ на задачу: 48,7845м 2 .
Вы можете округлить ответ до 48,8 м 2 или 49 м 2 .
См. нашу страницу по Оценка, приближение и округление .
HSPT Mathematics — HSPT Math
Все математические ресурсы HSPT
6 диагностических тестов
130 практических тестов
Вопрос дня
Карточки
Learn by Concept
← Предыдущая 1 2 … 207 208 209 210 211 212 213 214 215 Следующая →
HSPT Math Help »
HSPT Mathematics
Комната имеет размеры 18 на 15 на 9 футов.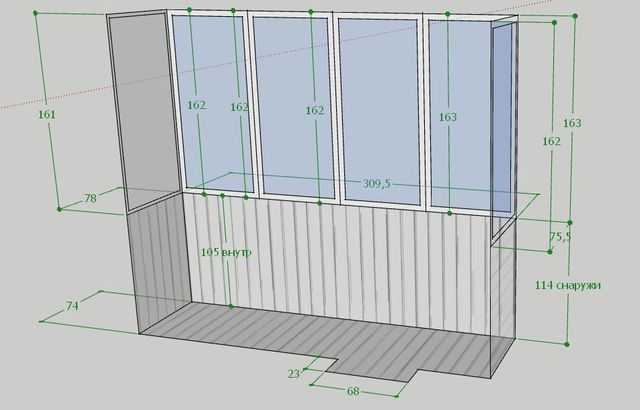 Последним размером является высота комнаты. В нем есть одна дверь размером 3 фута на 7 футов и два окна, каждое 2 фута на 5 футов. Нет отделки пола, стен, дверей и окон. Какова общая открытая площадь стены?
Последним размером является высота комнаты. В нем есть одна дверь размером 3 фута на 7 футов и два окна, каждое 2 фута на 5 футов. Нет отделки пола, стен, дверей и окон. Какова общая открытая площадь стены?
Possible Answers:
2389ft 2
594 ft 2
553 ft 2
1093ft 2
1134ft 2
Correct answer:
553 ft 2
Объяснение:
Если разбить на части, это простая задача. Сначала необходимо выделить размеры стен. Если высота комнаты 9 футов, мы знаем, что 18 x 15 обозначает площадь пола и потолка. Исходя из этого, мы знаем, что комната имеет следующие размеры по стенам: 18 х 9и 15 x 9. Так как каждой из них по две, мы можем вычислить общую площадь стен, не считая дверей и окон, удвоив сумму этих двух площадей:
2 * (18 * 9 + 15 * 9) = 2 * (162 + 135) = 2 * 297 = 594 фута 2
Теперь нам просто нужно вычислить площадь, «вынутую» из стен:
Для двери: 3 * 7 = 21 фут 2
Для окон: 2 * (2 * 5) = 20 футов 2
Таким образом, общая площадь стены составляет: 594 – 21 – 20 = 553 фута 2
Сообщить об ошибке
Комната имеет размеры 23 на 17 на 10 футов. Последним размером является высота комнаты. В нем есть одна дверь размером 2,5 фута на 8 футов и одно окно размером 3 фута на 6 футов. Нет отделки пола, стен, дверей и окон. Если одна банка краски покрывает 57 футов 2 площади поверхности. Сколько банок краски нужно купить, чтобы покрасить стены комнаты.
Последним размером является высота комнаты. В нем есть одна дверь размером 2,5 фута на 8 футов и одно окно размером 3 фута на 6 футов. Нет отделки пола, стен, дверей и окон. Если одна банка краски покрывает 57 футов 2 площади поверхности. Сколько банок краски нужно купить, чтобы покрасить стены комнаты.
Возможные ответы:
14
11
15
13
18
Правильный ответ:
14
Объяснение:
Если разбить на части, это простая задача. Сначала необходимо выделить размеры стен. Если высота комнаты 10 футов, мы знаем, что 23 x 17 обозначает площадь пола и потолка. Исходя из этого, мы знаем, что комната имеет следующие размеры по стенам: 23 х 10 и 17 х 10. Так как и тех и других по две, то можно вычислить общую площадь стен — без учета дверей и окон — путем удвоения суммы из этих двух областей:
2 * (23 * 10 + 17 * 10) = 2 * (230 + 170) = 2 * 400 = 800 футов
Для двери: 2,5 * 8 = 20 футов 2
Для окон: 3 * 6 = 18 футов 2
Таким образом, общая площадь стены составляет: 800 – 20 – 18 = 762 4 фута
Теперь, если одна банка краски покрывает 57 футов 2 , мы рассчитаем необходимое количество банок, разделив общую открытую площадь на 57: 762/57 = (приблизительно) 13,37.
Так как мы не можем купить неполные банки, мы должны купить 14 банок.
Сообщить об ошибке
Некоторый куб имеет длину стороны 25 м. Сколько квадратных плиток, каждая площадью 5 м 2 , необходимо, чтобы полностью покрыть поверхность куба?
Возможные ответы:
500
100
200
1000
750
Правильный ответ:
7503
Объяснение:
Куб со стороной 25 м имеет площадь поверхности:
25 м * 25 м * 6 = 3750 м 2
(Площадь поверхности куба равна площади одной грани куба, умноженной на на 6 сторон. Другими словами, если сторона куба равна с, , то площадь поверхности куба равна 6 с 2. )
Каждая квадратная плитка имеет площадь 5 м 2 .
Таким образом, общее количество квадратных плиток, необходимых для полного покрытия поверхности куба, составляет:
3750м 2 /5м 2 = 750
Примечание: объем куба со стороной s равен s 3 . Следовательно, если спросить, сколько мини-кубов со стороной n нужно заполнить исходный куб, ответ будет таким:
Следовательно, если спросить, сколько мини-кубов со стороной n нужно заполнить исходный куб, ответ будет таким:
s 3 /n 3
постройте кубическую комнату вокруг конуса так, чтобы высота и диаметр конуса были на 3 дюйма меньше, чем размеры куба. Если объем конуса 486π футов 3 , какова площадь поверхности куба?
Possible Answers:
69,984 in 2
486 in 2
513.375 in 2
73,926 in 2
726 in 2
Correct answer:
73 926 в 2
Пояснение:
Для начала нам нужно найти размеры конуса.
Базовая форма объема конуса: V = (1/3) πr 2 h
Используя наши данные, мы знаем, что h = 2r , потому что высота конуса соответствует его диаметру (на основе подсказки).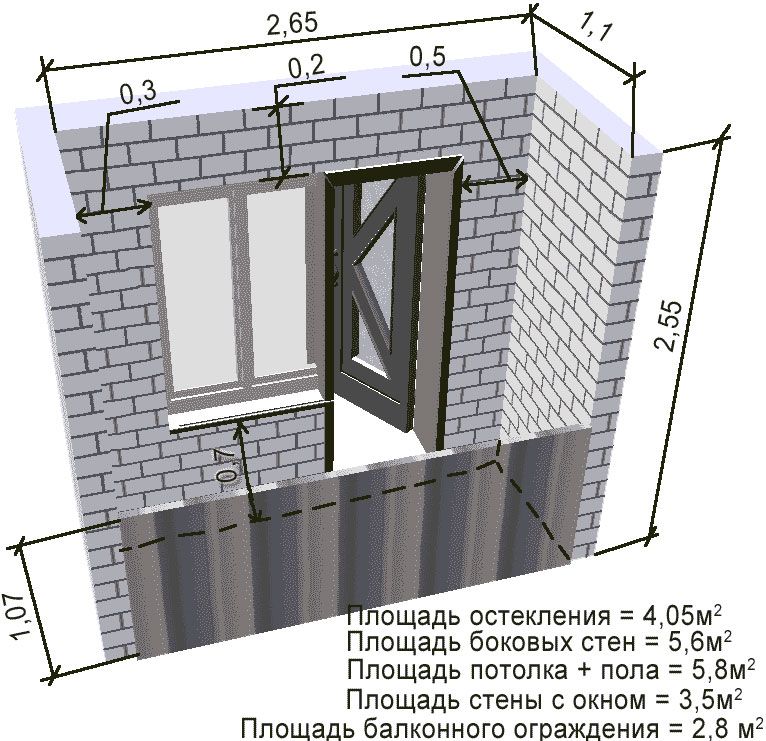
486 π = (1/3) πr 2 * 2 R = (2/3) πr 3
Многофункционал оба срока на (3/2 3
). 729 = r 3
Извлеките кубический корень из обеих сторон: r = 9
Обратите внимание, что это футов . Ответы в квадратных дюймах. Поэтому переведите единицы измерения в дюймы: 9 * 12 = 108, а затем добавьте к этому 3 дюйма: 108 + 3 = 111 дюймов.
Площадь поверхности куба определяется как: A = 6 * с 2 , или для наших данных, A = 6 * 111 2 = 73 9026 9005 2 в отчете 2 Ошибка
Энджи рисует двухфутовый куб для пьесы, в которой она участвует. Ей нужна краска на каждый квадратный фут, который она рисует. Сколько краски ей нужно?
Возможные ответы:
Невозможно преобразовать метрические единицы в футы.
Ни один из доступных ответов
Правильный ответ:
Пояснение:
Сначала мы должны вычислить площадь поверхности куба. Мы знаем, что есть шесть поверхностей и каждая поверхность имеет одинаковую площадь:
Мы знаем, что есть шесть поверхностей и каждая поверхность имеет одинаковую площадь:
Теперь определим необходимое количество краски
Сообщить об ошибке
Сферический апельсин плотно помещается в небольшой кубической коробке так, что каждая из шести стенок коробки едва касается поверхности апельсина. Если объем коробки 64 кубических дюйма, какова площадь поверхности апельсина в квадратных дюймах?
Возможные ответы:
16π
128π
64π
256π
32π
Правильный Ответ:
16*
0044
Пояснение:
Объем куба находится по формуле V = s 3 . Поскольку V = 64, s = 4. Сторона куба равна диаметру сферы. Поскольку d = 4, r = 2. Площадь поверхности сферы находится по формуле SA = 4π(r 2 ) = 4π(2 2 ) = 16π.
Сообщить об ошибке
Спальня Стива имеет размеры 20 на 18 на 8 футов в высоту.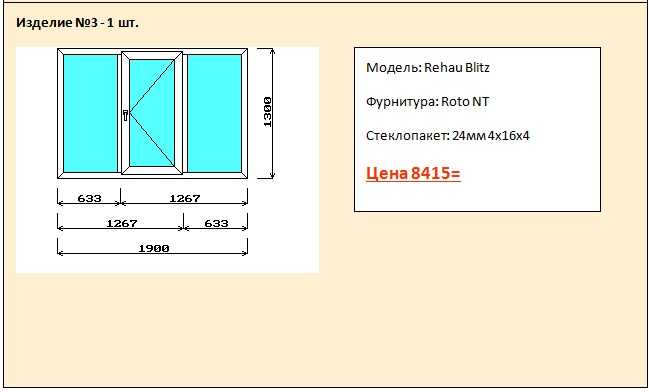 Он хочет покрасить потолок и все четыре стены краской, укрывающей 360 квадратных футов на галлон. Одногаллонная банка краски, которую хочет Стив, стоит 36 долларов; банка в одну кварту стоит 13 долларов. Какова наименьшая сумма денег, которую Стив может потратить на краску, чтобы покрасить свою комнату?
Он хочет покрасить потолок и все четыре стены краской, укрывающей 360 квадратных футов на галлон. Одногаллонная банка краски, которую хочет Стив, стоит 36 долларов; банка в одну кварту стоит 13 долларов. Какова наименьшая сумма денег, которую Стив может потратить на краску, чтобы покрасить свою комнату?
Возможные ответы:
Правильный ответ:
Объяснение:
У двух стен есть площадь ; у двух есть площадь; у потолка есть площадь.
Таким образом, общая площадь, которую Стив хочет покрыть, равна
Разделите 968 на 360, чтобы получить количество галлонов, необходимое Стиву для покраски своей спальни: банки или трехлитровые банки.
Первый вариант будет стоить ему ; второй вариант будет стоить ему . Последний вариант является более экономичным.
Сообщить об ошибке
Укажите площадь поверхности вышеуказанного ящика в квадратных сантиметрах.
Возможные ответы:
Правильный ответ:
Объяснение:
100 сантиметров составляют один метр, поэтому преобразуйте все размеры коробки, умножив их на 100.
сантиметры
сантиметры
Используйте формулу площади поверхности, подставив:
квадратные сантиметры
Сообщите об ошибке
Рисунок НЕ выполнен в масштабе.
См. рисунок выше, на котором изображен квадрат. Укажите отношение площади желтой области к площади белой области.
Возможные ответы:
Среди других вариантов правильного ответа нет.
Правильный ответ:
Объяснение:
Площадь всего квадрата – это квадрат длины стороны, или
.
Площадь прямоугольного треугольника равна половине произведения его катетов, или
.
Таким образом, площадь желтой области – это разность двух значений, или
.
Отношение площади желтой области к площади белой области равно
; то есть от 55 до 9.
Сообщить об ошибке
Выше изображен прямоугольный бассейн для квартиры. Бассейн везде пяти футов глубиной.
Управляющий квартирой хочет покрасить четыре стороны и дно бассейна. Одна галлонная банка краски, которую он хочет использовать, покрывает квадратные футы. Сколько банок краски нужно купить менеджеру?
Возможные ответы:
Правильный ответ:
Пояснение:
Дно бассейна имеет площадь
квадратных футов.
Есть две стороны площадью
квадратных футов,
и две стороны площадью
квадратных футов.
 д.) – 4–6 м2.
д.) – 4–6 м2. Жилище необходимо оснастить множеством инженерного оборудования: водяные очищающие фильтры, котлы, насосы. Чтобы разместить всю эту технику, к размерам частного дома нужно добавить отдельную комнату с оптимальной площадью – 4-5 м2.
Жилище необходимо оснастить множеством инженерного оборудования: водяные очищающие фильтры, котлы, насосы. Чтобы разместить всю эту технику, к размерам частного дома нужно добавить отдельную комнату с оптимальной площадью – 4-5 м2.
 Дверной блок состоит из двух одинаковых полотен. В летний сезон открывают обе створки, зимой одну фиксируют и пользуются только второй.
Дверной блок состоит из двух одинаковых полотен. В летний сезон открывают обе створки, зимой одну фиксируют и пользуются только второй.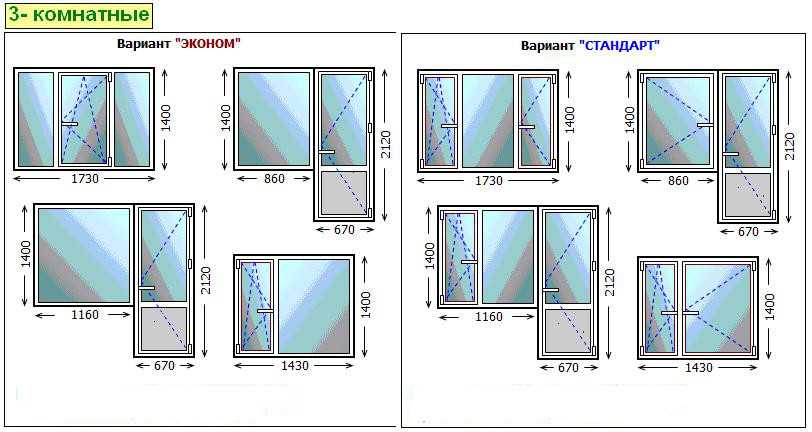 м.
м. м. После округления получаем 1,2 кв. м.
м. После округления получаем 1,2 кв. м.