Маятниковая петля: Фапиком – интернет магазин фурнитуры для дверей и окон в Санкт-Петербурге
Маятниковая петля Hafele для дверей весом до 27 кг
Наведите на картинку для увеличения
1 ОтзывНаписать отзыв
КОД:
927.01.270
Цена 1,100.92 грн
Доступность:
В наличии
Цвет:
Латунь
Никель
Бонусные баллы:
баллов
Кол-во:
+
−
+38(067) 382-55-77
- Описание
- Особенности
- Отзывы
- Видео галерея
Петля маятниковая двусторонняя, пружинная, для дверей весом до 27 кг с возможностью регулировки усилия пружины и скорости закрывания двери.
Для дверного полотна из древесины.
Предназначены, для дверей установленных внутри помещения.
Для двери весом: до 27 кг.
Толщина двери: 30-35 мм.
Материал: сталь.
Покрытие, цвет: никелированная.
С возможностью регулировки усилия пружины и скорости закрывания двери.
Высота: 125 мм.
Диаметр ролика: 22 мм.
Высота ролика: 147 мм.
Расстояние между осями роликов: 65 мм.
Максимальная высота двери: 2000 мм.
Максимальная ширина двери: 700 мм.
Зазор между дверным полотном и дверной коробкой: 12 мм.
Для дверного полотна из древесины.
Универсальные, правые и левые по DIN.
Петля для маятниковых дверей, открывание в две стороны, угол раскрытия: 180 градусов.
Бренд:
Hafele
Вага дверей:
27 кг
Вид петли по конструкции:
Маятниковая
Срок хранения:
Неограниченный
Страна-производитель:
Германия
Цвет:
Никель
Врезка и регулировка петли
Возможно вас это заинтересует
- Похожие товары
- Вы просматривали ранее
Быстро и качественно доставляем
Наша компания производит доставку по всей Украине
Гарантия качества и сервисное обслуживание
Мы предлагаем только те товары, в качестве которых мы уверены
Возврат товара в течение 14 дней
У вас есть 14 дней, для того чтобы протестировать вашу покупку
Маятниковые петли стеклянных дверей душевых кабин Pontere
Маятниковые петли для стеклянных дверей душевых кабин Pontere, крепление стекло -стена, стекло-стекло.
Двустороннее открытие — наружу и вовнутрь на 90º, 135º, 180º. Покрытие петель матовое, блестящее, нержавеющая сталь.
Таблицы основных характеристик петель стеклянных дверей
- петли стеклянных дверей — отличия и основные характеристики
- характеристики покрытий — петель и аксессуаров душевых кабин
- подбор петель от веса — стеклянной двери душевой кабины
| ||||||
| ||||||
| ||||||
| ||||||
| ||||||
| ||||||
| ||||||
| ||||||
:8408MS
:8414MS
:8410MSПрерванный маятник и петля-де-петля
Прерванный маятник и петля-де-петля
1 Прерванный маятник
Рассмотрим классическую задачу прерывистого маятника ,
как показано на рисунке 1. Это действительно
классика, опубликованная в 1638 году каким-то парнем по имени Галилей.
Рис. 1. Прерванный маятник
Традиционно известен под названием остановившийся маятник , но
это имя может сбить с толку.
Задача найти H max , максимальная высота, на которую поднимается боб,
в зависимости от начальных условий.
Вот сценарий: у нас есть строка, привязанная к какой-то точке
А.
На другом конце веревки маленький тяжелый боб, показанный
как черный диск на диаграмме. Это был бы обычный маятник,
за исключением того, что качание прерывается колышком в точке P.
В этом базовом сценарии есть много случаев и подслучай,
простоты мы рассматриваем только ту часть траектории, где
движение определяется штифтом – и гравитацией, и другими законами
физики. (Это исключает случаи, когда струна не попадает в колышек,
и где струна касается чего-то другого, кроме колка, и так далее.)
Мы делаем ряд дополнительных предположений, которые
«стандартным» в такого рода задачах, а именно, что строка
имеет пренебрежимо малую толщину, пренебрежимо малую массу и пренебрежимо малую
жесткость. Предположим, что точки P и A зафиксированы. Мы предполагаем
шпилька имеет незначительный размер. Мы пренебрегаем всеми формами
трение.
Нам не нужно предполагать, что якорь A находится прямо над штифтом P.
Как следствие предыдущих предположений, мы не заботимся о
масса боба.
(Если не верите, можете переделать
расчет с сохранением M в качестве явного параметра. Убедитесь, что
окончательный ответ нечувствителен к M.) Таким образом, WLoG («Без потери
общность»), мы можем установить M=1.
Также, как следствие предыдущих предположений, нас не волнует
общая длина строки; все, что нам нужно, это длина L
от колышка до боба. Кроме того, WLoG мы выбираем наши единицы измерения
длина такая, что L=1, поэтому L также выпадает из задачи.
Аналогично WLoG мы выбираем единицы времени так, чтобы ускорение
гравитация g=1.
Мы определяем угол θ как угол струны относительно
вниз по вертикали, как показано на схеме.
Мы определяем H как высоту боба относительно колышка.
Потенциальная энергия боба U пропорциональна высоте. WLoG мы
используем наш выбор калибровки так, чтобы H=0 соответствовало U=0. (Мы
не обязательно предполагают, что боб когда-либо достигнет этой высоты;
это всего лишь наш «эталонный» уровень.) Очевидно, что U — это
функция времени.
Как следствие предыдущих предположений, U равно
не только пропорциональна H, но и равна H. То есть U=H
всегда.
Примечание: В случаях, когда нить не провисает, мы можем
запишем U = −M g L cos(θ) … или ввиду
предыдущие упрощения, просто U = H = -cos (θ).
Однако, если вы не знаете о синусе и косинусе, вы можете
игнорировать это замечание; тригонометрия не требуется, чтобы решить это
проблема.
Боб имеет кинетическую энергию K. Очевидно, что K является функцией времени.
Полная энергия боба E = U + K. Это сохраняющаяся величина,
независимо от времени.
1.1 Случай низкой энергии
Начнем с рассмотрения случая низкой энергии, такого, что |θ|
остается меньше 90 градусов. Наши общие знания о маятниках говорят
Нам известно, что в этом случае струна не провиснет. Это также говорит нам
что боб останавливается на вершине качания. То есть К=0 при
верх качелей. Поэтому мы имеем простой результат, что
| H max = E для E ∈ [−1, 0] (1) |
1.
2 Корпус с высоким энергопотреблением
С другой стороны, корпус с высоким энергопотреблением также прост. Если
есть много энергии, боб идет прямо сверху, и
струна мотается вокруг колышка, никогда не провисая.
Нам нужно рассчитать минимальную энергию, соответствующую этому результату.
Достаточно рассмотреть, что происходит в самом начале движения,
в точке непосредственно над колышек. Будет определенная сумма
центробежного ускорения, C. Нам нужно, чтобы C было не менее
1g, чтобы поддерживать неотрицательное натяжение струны.
Оказывается, что C = 2K в маргинальном случае высоких энергий, как вы
можно проверить, рассмотрев известные выражения K = ½ M v 2
и F C = M v 2 / L. Следовательно, в верхней точке качания боб
должна иметь полную энергию E = 1,5 (половину единицы кинетической энергии, чтобы
держать струну в натянутом состоянии, плюс одну единицу потенциальной энергии).
То есть:
| H max = 1 для E ≥ 1,5 (2) |
1.
3 Предвосхищение
На данный момент мы уже знаем достаточно, чтобы проделать довольно хорошую работу
отвечая на поставленный вопрос, зарисовывая H max как функцию
энергии. Это показано на рисунке 2.
Рисунок 2. Максимальная высота в зависимости от энергии
Мы знаем точное решение для E в интервале [−1, 0], а именно
H max = E, как обсуждалось в разделе 1.1. Мы также знаем
точное решение для E больше 1,5, как обсуждалось в
раздел 1.2.
Мы можем довольно точно начертить кривую в промежуточной области,
так как мы ожидаем, что это будет гладкая функция от E. На самом деле, мы можем
использовать кубический сплайн, определяемый условиями единичного наклона на
точка (0, 0) и нулевой наклон в точке (1,5, 1). Прямо сейчас это
это всего лишь оценка, но она оказывается очень хорошей оценкой,
как мы увидим в следующем разделе.
1.4 Slack Case
Теперь давайте рассмотрим промежуточный случай, показанный красным на
рисунок 2.
Это тот случай, когда строка идет
слабину до того, как боб достигнет максимальной высоты.
Давайте проанализируем момент, когда струна впервые начинает провисать.
Эта точка определяется тем критерием, что составляющая
гравитационное ускорение в направлении струны
уравновешивает центробежное ускорение. Этот радиальный
компонент — это просто g H или просто H в единицах измерения, которые мы используем.
Вы можете получить этот результат с помощью тригонометрии (−g cos(θ) =
г ч). Вы также можете вывести его без тригонометрии, просто используя
рассуждения о подобных треугольниках.
И снова центробежное ускорение равно 2K, что равно
2Э — 2Н. Давайте использовать S для обозначения специальной высоты, на которой
струна начинает провисать. Приравнивание радиальной составляющей силы тяжести
центробежному ускорению, находим
| ( 3) |
Вы можете убедиться, что этот результат согласуется с тем, что мы уже
знаю происходит при E=0 и E=1,5.
В тот момент, когда струна начинает провисать, грузик имеет некоторую скорость
v. Нам не нужно вычислять v, но мы знаем, что v имеет горизонтальную
компонент и вертикальный компонент. Горизонтальная составляющая
пропорциональна Н; когда H=0, горизонтальная составляющая равна нулю, а
когда H=1, горизонтальная составляющая составляет 100% скорости.
Таким образом, горизонтальная часть кинетической энергии пропорциональна
Н 2 .
Это означает, что мы можем записать кинетическую энергию как
| K = (H 2 ) K + (1−H 2 )K (4) |
, где первый член в правой части связан с горизонтальным движением, и
второй член обусловлен вертикальным движением. В частности, на
В точке, где струна начинает провисать, полная энергия равна:
| (5) |
где мы использовали тот факт, что K=S/2 из уравнения 3.
В верхней точке качелей нет вертикальной скорости, а высота
равно H max , поэтому энергия равна
| E = H макс. + (S 2 ) S/2 (6) |
где последний член представляет горизонтальную кинетическую энергию, которая
есть постоянная движения, когда струна натянута.
Сравнивая уравнение 5 с уравнением 6, находим
что
| H max = S + ½ S(1−S 2 ) для S ∈ [0,1] (7) |
, где S = (2/3)E. Вы можете убедиться, что эта функция проходит через
точек (E, H max ) = (0, 0) и (1,5, 1) и имеет ожидаемый наклон
в каждом случае (наклон = 1 и наклон = 0 соответственно).
1.5 Резюме
Теперь мы ответили на исходный вопрос. Уравнение 1,
уравнение 7 и уравнение 2 охватывают все
возможности. Это показано на рисунке 2.
Теперь мы можем подтвердить, что сплайн, предполагаемый в
раздел 1.
3 был абсолютно правильным.
Галилей прежде всего интересовался низкоэнергетическим случаем. Он также был
вполне осведомлен о высокоэнергетическом (обтекающем) корпусе. Я не в курсе
что он когда-либо отрабатывал промежуточный (слабый) случай.
2 Поездка по петле-де-петле
Ради интереса теоретически рассмотрим ускорения
опыт наблюдателя, катающегося на качелях с очень большим
амплитуда, достаточно большая, чтобы полностью выйти за пределы — или,
то же самое, наблюдатель в самолете, выполняющий петлю за петлей.
Примечание! Это неполный теоретический анализ, описывающий
Только мысленный эксперимент. Не пытайтесь сделать это с
что-то большее, чем маленькая игрушка, если вы не сделали
полный анализ, включая все практические вопросы.
Не пытайтесь делать это на реальном самолете, если вы не получили
тщательная пилотажная подготовка от сертифицированного пилота-инструктора.
Вы несете ответственность за понимание рисков и выполнение
полный анализ, включая запасы прочности.
Для качелей важно учитывать крайний случай, когда
у боба едва хватает энергии, чтобы ходить по кругу без
идет вяло. В верхней части качелей наблюдатель находится в невесомости (в
его рама, то есть рама, сопутствующая бобу). Это можно подумать
как один г обычной земной гравитации, противостоящей одному г
центробежное ускорение в противоположном направлении. Боб имеет 0,5
ед. кинетической энергии в этой точке и 1,5 ед. полной
энергия.
Теперь мы продолжаем траекторию до самого низа. В пути
вниз, боб получает две единицы кинетической энергии, в сумме
2.5, и, следовательно, наблюдатель испытает шесть g
ускорение вниз: пять g центробежного ускорения плюс один
g земного притяжения в том же направлении.
Это означает, что если вы хотите выполнить петлю за петлей, в
приближение постоянной энергии, не поддерживающее люфт все время
наоборот, вы должны быть готовы выдержать шесть Джи внизу
… чего достаточно, чтобы быть весьма заметным!
Немаргинальный случай также возможен.
Если в системе больше
энергии, струна будет больше натянута по всему периметру.
Если вы замените струну распоркой, вы можете получить нулевой
скорость в верхней точке качания. В этом случае вы потянете как минимум
пять g внизу в приближении постоянной энергии.
Запасной маятник с петлей — ¾» — Коммерческие комплекты качелей
Ищете запасной маятник? Мы предлагаем вам прочный вариант шириной 3/4″. Оснащен масляным подшипником с внутренним диаметром 0,51, осевым болтом с замком. Этот маятник идеально подходит для использования в оборудовании для игровых площадок.Обратите внимание, что гайка и болт в комплект не входят.Срок службы до 5 лет в оптимальных условиях. суровых условиях и может похвастаться впечатляющей прочностью на растяжение в 12800 фунтов.Хотя в определенных условиях может потребоваться более ранняя замена, будьте уверены, что наш сменный маятник рассчитан на долгий срок службы.0007
**Инструкции по установке, безопасному использованию и техническому обслуживанию**
ВАЖНО: Прочтите важную информацию.
В этом материале мы попытались представить некоторые требования, изложенные в справочниках CPSC, ASTM F2373-11, F1487-11 и F1148-09. Тем не менее, мы ни в коем случае не хотим, чтобы это был полный список требований. Кроме того, эти публикации часто обновляются с изменениями, поэтому вам следует самостоятельно прочитать эти публикации, чтобы определить, может ли какая-либо часть или установка представлять опасность для ребенка.
Чтобы уберечь детей от травм, перед установкой оборудования ознакомьтесь с инструкциями по установке и обслуживанию. Они находятся в описании каждого товара на нашем сайте. www.americanswing.com Загрузите и распечатайте эти инструкции и сохраните их в надежном месте. На нашем веб-сайте также есть страница «Информация о тестировании продукта». Все продукты тестируются на содержание свинца, фталатов и прочность на растяжение. Вы также можете позвонить нам по телефону 1-800-433-2573 для получения дополнительной информации или посетить http://www.cpsc.gov/cpscpub/pubs/325.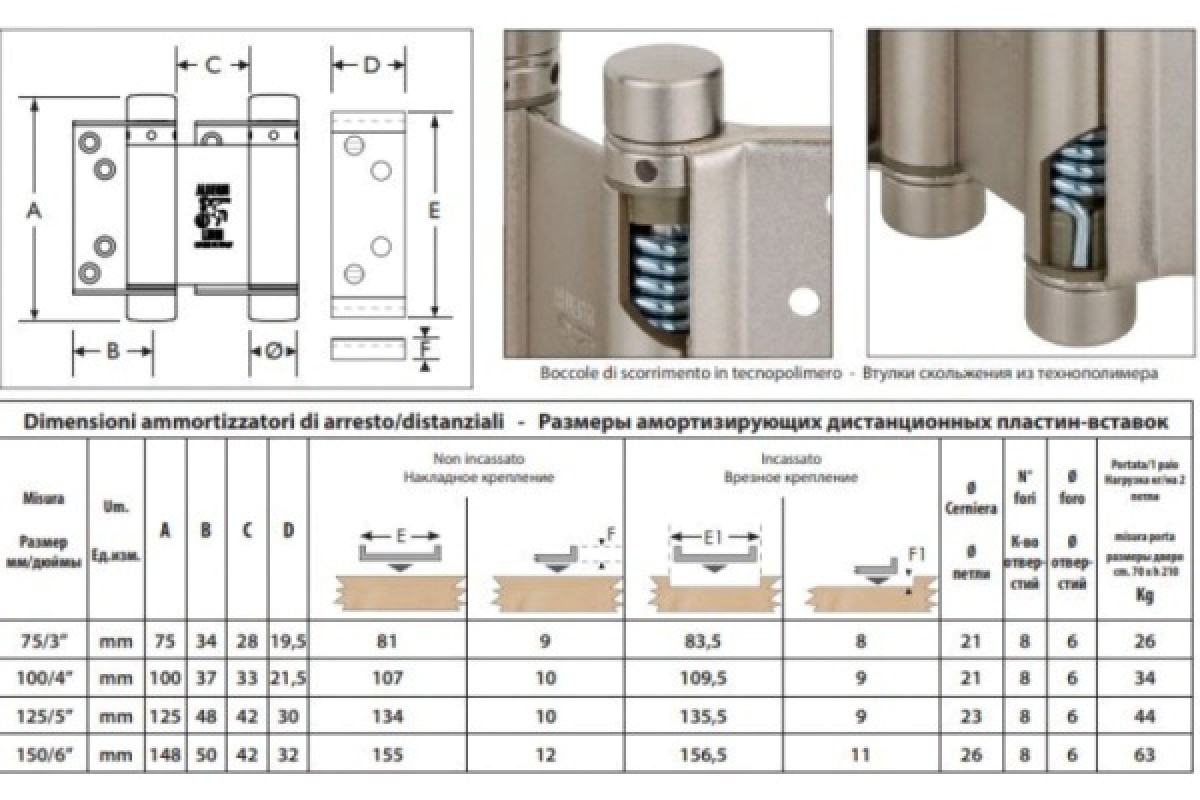
pdf.
Установка: Наши детали продаются либо как запасные части, либо как компоненты комплекта, если только вы не покупаете наш комплект металлической рамы, поэтому эти детали необходимо устанавливать в соответствии с инструкциями по установке комплекта. Если инструкции по установке отличаются от наших, свяжитесь с нами по телефону 800-433-2573.
Выньте болт из подвески качания, чтобы заменить старый маятник новым. Убедитесь, что когда вы вставляете болт обратно через втулку в маятник, гайка плотно прилегает. После затяжки резьба не должна выходить за пределы гайки более чем на два витка. Вам нужно будет использовать S-образные крюки или скобы от цепи до вешалок для качелей. Убедитесь, что S-образные крюки закрыты с точностью до 0,04, чтобы соответствовать стандартам безопасности ASTM. Для этого вам понадобятся наши плоскогубцы с S-образным крючком или обычные плоскогубцы для замков каналов. ПРЕДУПРЕЖДЕНИЕ. После открытия S-образных крюков их необходимо заменить, чтобы избежать травм в результате открытия и/или поломки.
При использовании H-образной скобы большой конец проходит через подвеску для качелей. Использование гаечного ключа A5750 для открывания и закрывания болтов. Убедитесь, что если вы используете скобы, они также затянуты. Все крепления должны быть закрыты согласно рисунку A1.19..
Безопасное использование: Только для детей в возрасте от 0 до 12 лет. Взрослые должны постоянно присматривать за детьми. Не позволяйте детям использовать небезопасно. Не допускайте его использования, если он поврежден.
Техническое обслуживание: В начале и в конце каждого игрового сезона и раз в месяц во время игрового сезона проверяйте подвеску на наличие острых краев и/или трещин, уделяя особое внимание поверхности вокруг отверстий для болтов. Проверьте, не изношен ли или не треснул ли масляный подшипник в маятнике поворотной подвески. При износе или наличии трещин замените маятник. Проверить на вандализм. При необходимости замените детали. Убедитесь, что стопорные гайки затянуты.