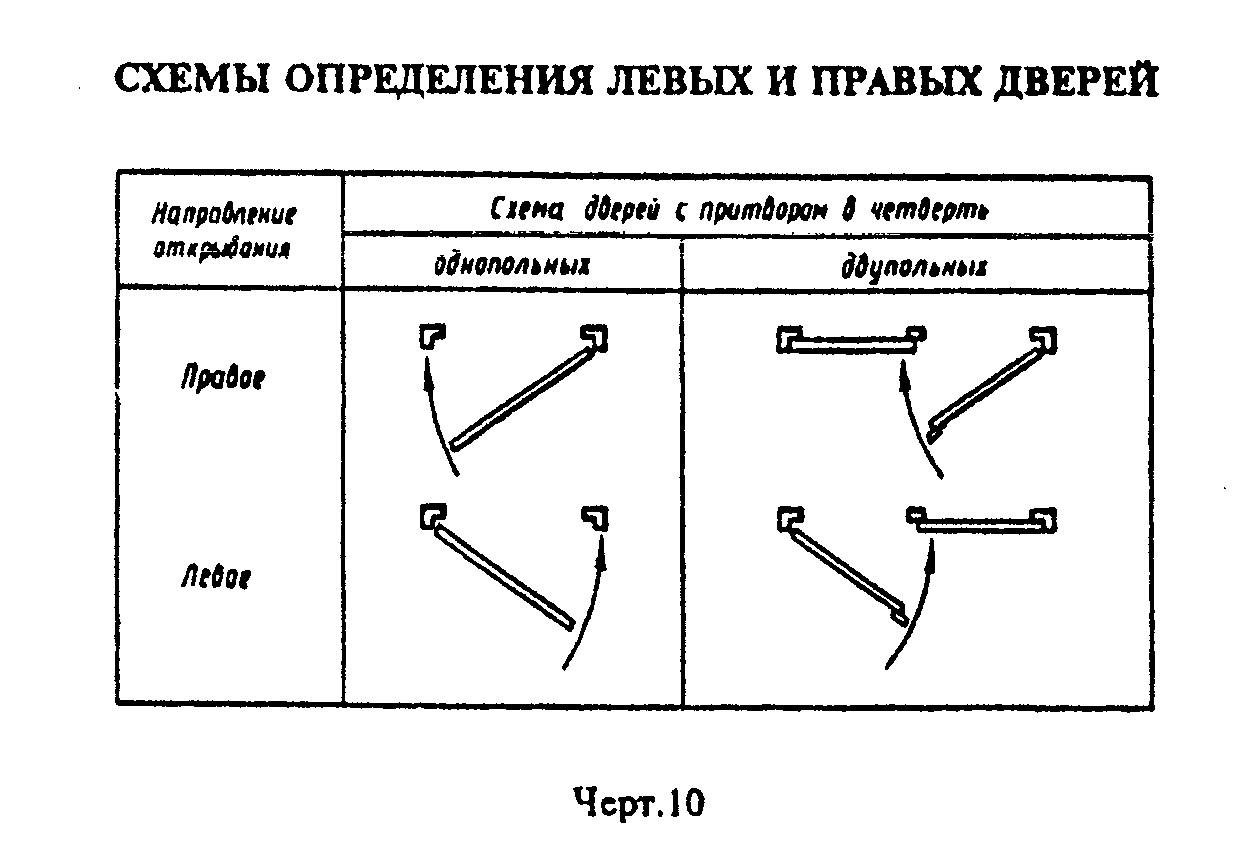
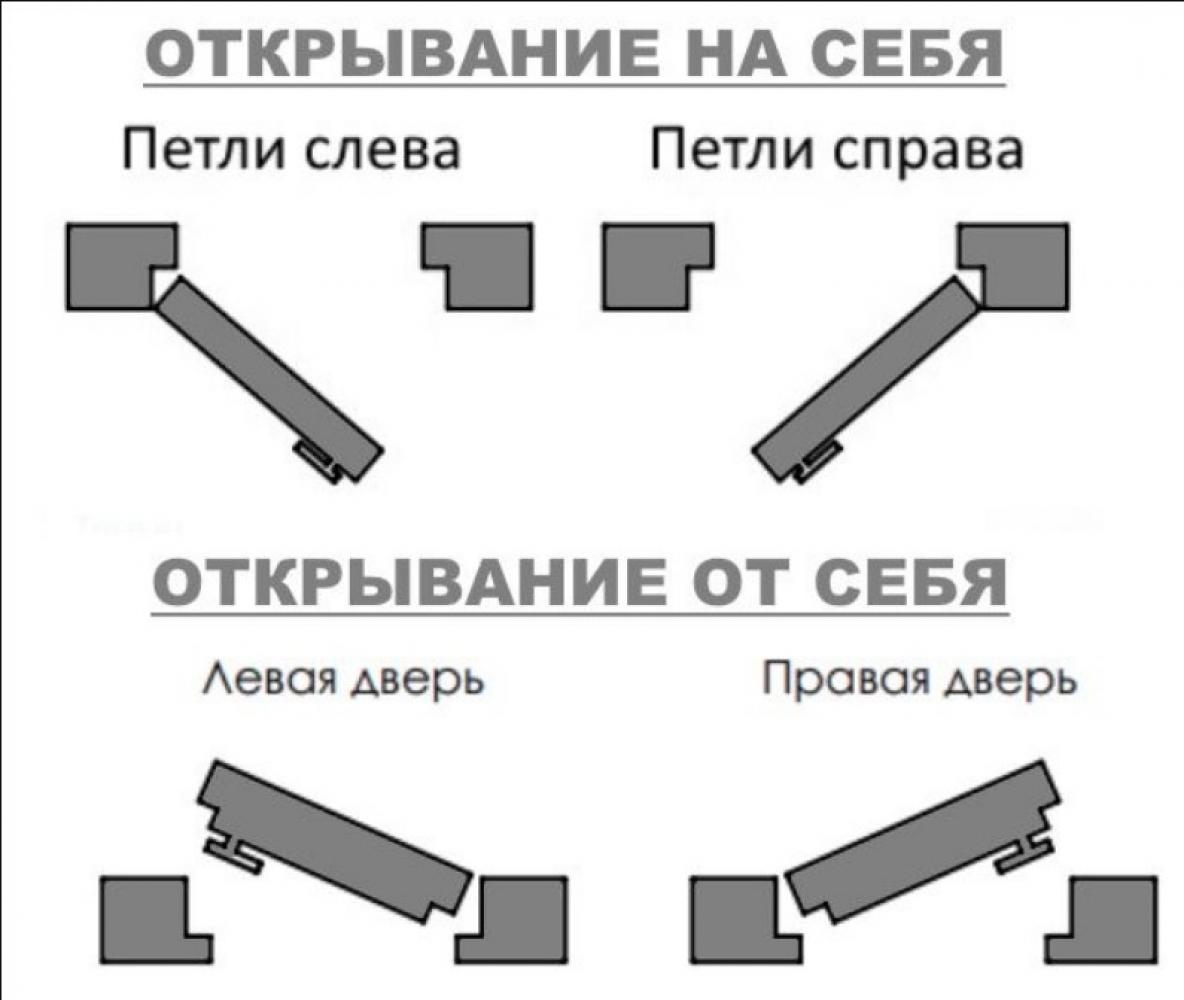
Открывание левое: Дверь правая или левая? Как определить открывание двери
- Заложенность уха — причины появления, при каких заболеваниях возникает, диагностика и способы лечения
- Автозапчасти в России, каталог автозапчастей, запчасти для иномарок
- 404 — СТРАНИЦА НЕ НАЙДЕНА
- 8.4: Парабола — Математика LibreTexts
Заложенность уха — причины появления, при каких заболеваниях возникает, диагностика и способы лечения
Грибок
Аллергия
Серная пробка
Отит
Аденоиды
Тугоухость
Ринит
Опухоль
760
04 Февраля
Заложенность уха: причины, диагностика и способы лечения.
Определение
Заложенность уха или ушей возникает как из-за нарушения звуковосприятия и характеризуется различными ощущениями, в числе которых могут быть глухота, чувство сдавливания и тяжести, слишком сильное звучание собственного голоса. Заложенность уха, независимо от причин ее возникновения, тяжело переносится пациентом и, как правило, требует помощи специалиста.
Заложенность уха, независимо от причин ее возникновения, тяжело переносится пациентом и, как правило, требует помощи специалиста.
Разновидности заложенности уха
Заложенность одного или обоих ушей может сопровождаться болью, покалыванием, шумом или звоном в ушах, головокружением. В некоторых случаях заложенность исчезает после акта глотания.
Опасным симптомом считается заложенность уха с присоединением повышенной температуры тела, головной боли, выделений из уха (гнойных или кровянистых), ощущения инородного тела.
Заложенность уха не всегда свидетельствует о патологическом процессе. Такое состояние может быть вызвано попаданием в ухо воды, перепадом давления во время воздушного перелета или погружения на глубину. Иногда слишком сильное и неправильное высмаркивание одновременно из двух носовых ходов приводит к закладыванию уха (ушей), что связано с повышением давления в средней камере уха вследствие резкого поступления воздуха из евстахиевой трубы. Прием некоторых лекарственных препаратов (антибиотиков, психотропных веществ) оказывает токсическое действие на ухо, провоцируя развитие заложенности и тугоухости.
Прием некоторых лекарственных препаратов (антибиотиков, психотропных веществ) оказывает токсическое действие на ухо, провоцируя развитие заложенности и тугоухости.
Заболевания, при которых может развиться заложенность уха
Серная пробка, закупорившая слуховой проход. Попытки удалить ушную серу самостоятельно при помощи подручных предметов значительно увеличивают вероятность проталкивания пробки глубже в ухо и налипания серы на барабанную перепонку (при этом повышается риск травмирования барабанной перепонки, что ведет к полной или частичной потере слуха). В этих случаях состояние заложенности в ушах сопровождается мучительной болью, шумом, головокружением и тошнотой.
Микотическое, или грибковое, поражение наружного слухового прохода. Инфицирование грибами может осложняться сужением или закупоркой слухового прохода с появлением чувства заложенности ушей. Усугубляют процесс распространения грибков в ухе слуховые аппараты, наушники-вкладыши, а также воспалительные заболевания уха. Основные признаки заболевания – зуд, заложенность уха и вызванная ею тугоухость, усиление в больном ухе звука собственного голоса.
Основные признаки заболевания – зуд, заложенность уха и вызванная ею тугоухость, усиление в больном ухе звука собственного голоса.
Повреждение наружного слухового прохода и структур среднего уха могут сопровождаться нарушением слуха и заложенностью. Кровотечение и формирование кровяного сгустка, который закупоривает слуховой проход, приводят к ухудшению звукопроводимости. Кроме того, возможна травма барабанной перепонки во время чистки слухового прохода, резкого перепада давления, сильного удара по наружному уху. При этом возникает резкая боль, которая сменяется заложенностью, звоном, шумом и нарушением слуха.
Острые воспалительные заболевания сопровождаются отеком, а иногда и образованием гнойного содержимого. Они могут приводить к заложенности уха и тугоухости. В частности, при отите среднего уха (тимпаните) в воспалительный процесс вовлекаются барабанная полость и слуховая труба. Отек, сужающий просвет слуховой трубы, и нагноение мягких тканей вызывают заложенность уха и нарушение слуха.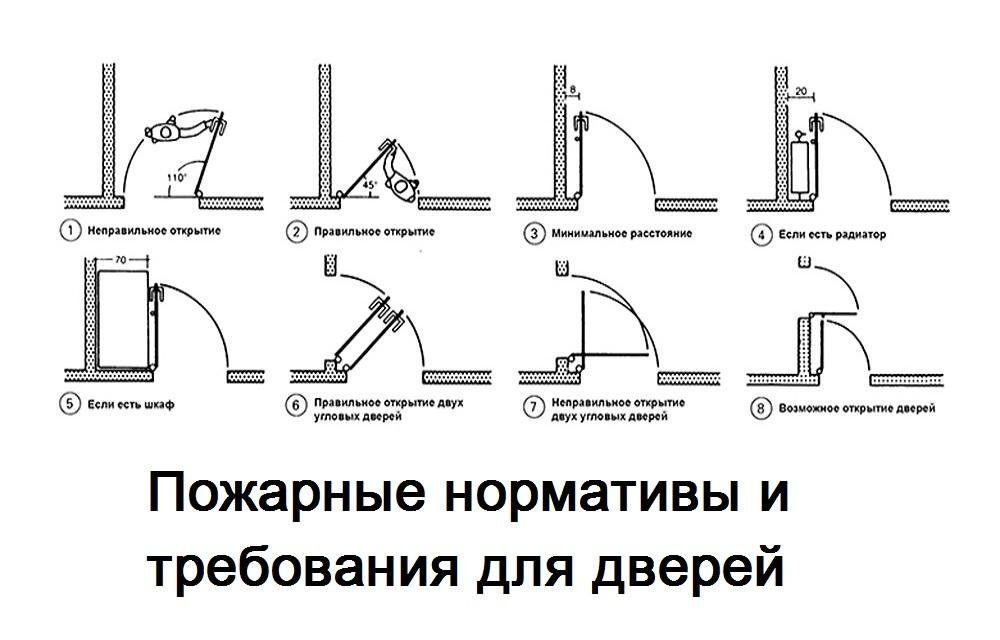 Как правило, инфекция проникает внутрь этой стерильной полости из евстахиевой трубы, которая напрямую связана с носоглоткой.
Как правило, инфекция проникает внутрь этой стерильной полости из евстахиевой трубы, которая напрямую связана с носоглоткой.
У детей первого и второго года жизни острый отит может возникнуть при попадании грудного молока или молочной смеси в носоглотку во время срыгивания.
У детей более старшего возраста отит среднего уха и заложенность могут быть вызваны воспалением аденоидов – лимфоидной ткани, отвечающей за местный иммунитет носоглотки и закрывающей отверстия слуховых труб в носоглотке. Анатомическая близость аденоидов и слуховой трубы обеспечивает быстрый переход инфекции из носоглотки в уши. Кроме того, увеличенные аденоиды могут перекрывать собой отверстия слуховой трубы, что вызывает чувство заложенности.
Аллергические реакции также могут приводить к острому воспалению и отеку среднего уха.
Отит наружного уха характеризуется воспалением наружного слухового прохода. Заложенность в ухе в этом случае возникает из-за отека тканей слухового прохода.
Если заболевание вызвано попаданием инородного тела в слуховой проход, то отек и заложенность дополняются картиной сильного раздражения. Пациент жалуется на сильный зуд, боль, чувство распирания, жар в области уха. Боль усиливается при жевательных движениях.
При фурункулезе наружного слухового прохода картина болезни усугубляется замкнутым пространством, где развивается воспалительный процесс. Нарастающая боль в ухе дополняется ее иррадиацией в соответствующую половину головы. Пациент не может лежать на больной стороне. Из-за сильного отека тканей наружного слухового прохода звукопроведение в больное ухо нарушается, возникает чувство заложенности.
К числу анатомических и послеоперационных дефектов, которые вызывают заложенность уха, относятся искривление перегородки носа, сужение носового хода вследствие гипоплазии крыльев носа, стеноз наружного клапана носа.
Нарушение носового дыхания ведет к частому появлению насморка, инфицированию носовых пазух и, как следствие, к переходу воспалительного процесса в слуховую трубу.
Заложенность уха в этих случаях появляется на стороне узкого носового хода. Такие же последствия возникают после операций в области носа.
Нейросенсорная тугоухость возникает из-за поражения какого-либо участка слухового нерва. Чаще всего это необратимое явление, симптомы которого включают нарушение равновесия, головокружение, тошноту, заложенность и шум в ухе, плохое восприятие низких звуков. Причинами нейросенсорной тугоухости могут быть перенесенные инфекционные и сосудистые заболевания, опухолевые процессы, травмы, токсическое воздействие различных веществ.
Болезнь Меньера — это негнойное заболевание внутреннего уха, которое сопровождается его заложенностью. Увеличение объема лимфы в лабиринте уха ведет к повышению давления и приступам прогрессирующей глухоты, возникновению шума в ушах, внезапного головокружения. В большинстве случаев сначала поражается одно ухо. Начинается заболевание либо с приступов головокружения, либо с ухудшения слуха, который между приступами полностью восстанавливается. Однако через несколько лет потеря слуха становится необратимой.
Однако через несколько лет потеря слуха становится необратимой.
Миофасциальный болевой синдром, заболевания височно-нижнечелюстного сустава. Пациенты с миофасциальным болевым синдромом, который связан с нарушением деятельности жевательной мускулатуры и ограничением подвижности нижней челюсти, также могут жаловаться на заложенность уха. Кроме того, заболевание сопровождается головными и лицевыми болями, затрудненным открыванием рта, щелканьем в области височно-нижнечелюстного сустава.
Первопричиной синдрома служит спазм жевательных мышц. Сходную клиническую картину дают также заболевания самого сустава, вызванные нарушениями прикуса.
Атеросклероз сосудов головного мозга, подъем артериального давления. Заложенность в ушах при поражении или сужении сосудов объясняется ухудшением кровоснабжения всех тканей, а также нарушением кровообращения в области внутреннего и среднего уха.
Вазомоторный ринит, или насморк при беременности возникает под влиянием гормональных сдвигов и характеризуется нарушением тонуса сосудов и выделением слизистого секрета. При аллергическом рините клиническая картина заболевания почти такая же, но провоцирующим фактором служат не гормоны, а специфический аллерген. Отек слизистой оболочки и сужение носовых ходов приводят к нарушению проходимости слуховой трубы и вызывают заложенность уха.
При аллергическом рините клиническая картина заболевания почти такая же, но провоцирующим фактором служат не гормоны, а специфический аллерген. Отек слизистой оболочки и сужение носовых ходов приводят к нарушению проходимости слуховой трубы и вызывают заложенность уха.
Опухоли в области слухового прохода, слуховой трубы и внутреннего уха – наиболее грозная причина возникновения заложенности уха. В их числе следует назвать холестеатому – опухолевидное образование, которое состоит из клеток эпидермиса, пропитанных холестерином. Холестеатома отличается медленным, но неуклонным ростом. Образуясь в среднем ухе, она может распространяться на наружное и внутреннее ухо, вызывая заложенность и чувство тяжести в ухе, гнойные выделения, отек и покраснение ушной раковины.
К каким врачам обращаться при заложенности уха
При возникновении заложенности уха следует обратиться к оториноларингологу. В дальнейшем может понадобиться консультация
терапевта,
педиатра,
гинеколога, невролога, кардиолога, аллерголога.
Диагностика и обследования при заложенности уха
Для диагностики заболевания, которое вызвало заложенность уха, необходим внимательный опрос пациента, осмотр наружного уха и слухового прохода до барабанной перепонки, аудиометрическое исследование. Инфекционную природу заболевания определяют на основе клинической картины, данных отоскопии и посева отделяемого.
Травма в области уха диагностируется с помощью рентгенографиии КТ.
Рентген черепа
Рентгенологическое исследование черепа для выявления нарушений структуры и целостности костей черепа различной природы.
2 290 руб
Записаться
Диагностику холестеатомы врач проводит на основании данных отоскопии и лучевых методов (рентгенографии и компьютерной томографии). Миофасциальный синдром и нарушение функции височно-нижнечелюстного сустава диагностируют по данным рентгенографии и КТ суставов, а также электромиографии.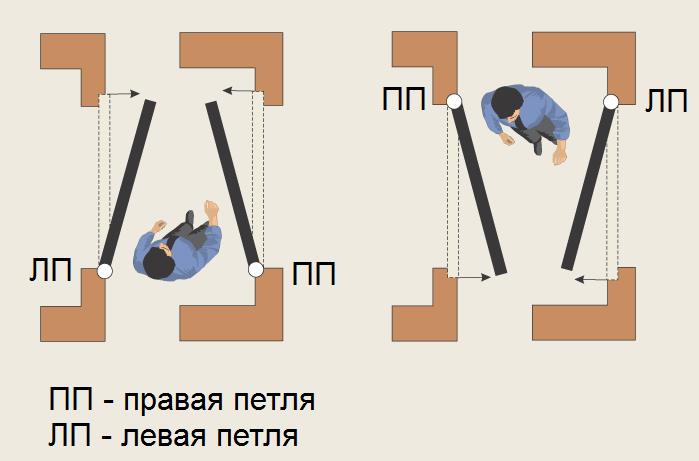
Что делать при заложенности уха?
Если заложенность уха возникает регулярно, не следует откладывать визит к врачу или пытаться самостоятельно устранять это состояние.
Лечение заложенности уха
Устранение заложенности уха возможно только при лечении вызвавшего ее заболевания.
В случае его инфекционной природы необходима антибиотикотерапия, противовоспалительная и обезболивающая терапия. Миофасциальный синдром и дисфункция височно-нижнечелюстного сустава требуют коррекции прикуса и противовоспалительного лечения. При опухолях и травмах в области уха показано хирургическое лечение. При неврологической и сосудистой природе заложенности и тугоухости подключают сосудистую и витаминотерапию.
Источники:
- Клинические рекомендации «Наружный отит» (дети). Разраб.: Союз педиатров России, Национальная медицинская ассоциация оториноларингологов, Межрегиональная ассоциация по клинической микробиологии и антимикробной химиотерапии.
 – 2021.
– 2021. - Клинические рекомендации «Наружные отиты» (взрослые). Разраб.: Национальная медицинская ассоциация оториноларингологов. – 2021.
- Клинические рекомендации «Отит средний острый». Разраб.: Национальная медицинская ассоциация оториноларингологов. – 2021.
- Болезнь Меньера: Клинические рекомендации. – Национальная медицинская ассоциация оториноларингологов. – Москва – Санкт-Петербург, 2014.
- Сенсоневральная тугоухость у взрослых: Клинические рекомендации. – Национальная медицинская ассоциация оториноларингологов. — Москва, 2016.
ВАЖНО!
Информацию из данного раздела нельзя использовать для самодиагностики и самолечения. В случае боли или иного обострения заболевания диагностические исследования должен назначать только лечащий врач. Для постановки диагноза и правильного назначения лечения следует обращаться к Вашему лечащему врачу.
Для корректной оценки результатов ваших анализов в динамике предпочтительно делать исследования в одной и той же лаборатории, так как в разных лабораториях для выполнения одноименных анализов могут применяться разные методы исследования и единицы измерения.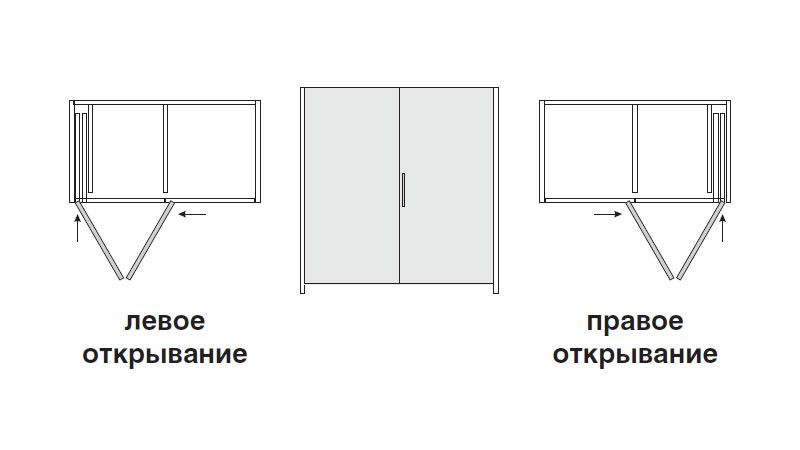
Автозапчасти в России, каталог автозапчастей, запчасти для иномарок
Поиск новых и б/у запчастей с разбора в России
По номеру запчастиПо VIN автомобиляПо автомобилю
по оригинальным каталогам
Найдите модель по Vin-номеру
VIN автомобиля является самым надежным идентификатором. Если ищете японский автомобиль, то введите FRAME
Выберите модель по параметрам
Если не помните VIN-номер, то воспользуйтесь поиском по параметрам в оригинальных каталогах
Очистить
Подробнее
Как заказать
запчасти на сайте
Узнать
Подписывайся
на наш TikTok
Перевозим грузы до 3 тонн
Подписывайся на наш
YouTube канал
В наличии
550 ноускатов — передняя часть в сборе
Выбрать
В наличии
Салоны — комплекты сидений
Выбрать
Машины на разбор
В ближайшее время ожидается новое поступление машин на разбор
XA154
AN194
W345
W342
W348
W347
W346
Honda CRV 2
Внедорожник 5дв. — 140 л.с.
— 140 л.с.
2005
W343
AN193
XA153
Выберите марку автомобиля
Легковые
Грузовые
Популярные категории
Все запчасти, представленные в каталоге, есть в наличии на складе и могут быть отправлены в кратчайшие сроки.
Mercedes ML или на что способен первый немецкий кроссовер
В 90-е годы в немецком автопроме отсутствовал такой класс как «кроссоверы». Его первенцем можно считать Mercedes ML в кузове W163, появившийся в 1997-м году.
11.07.202311
Освежи свое авто летними скидками!
Друзья! Мы запускаем скидки до 60% на все лето! Успей обновить свою красотку до конца августа!
10. 07.20232
07.20232
Audi A4 – в чем секрет живучести
Перед нами «живучее» Audi А4, являющееся кровным родственником Audi A6 и Passat В5, но выполненное в кузове С5. Почему она такая долго живучая, мы узнаем ниже. Временной период выпуска Audi А4 2001-2005 далее с конвейера стали сходить представители 3-го поколения. Кузов стал В7, что представляет собой глубокий рестайлинг В6. В модельном ряду, помимо ставших привычными универсала и седана, появляется кабриолет. К слову, Audi А4 основа в Seat Exeo, который выпускался до 2013 и считался испанским седаном.
10.07.202317
404 — СТРАНИЦА НЕ НАЙДЕНА
Почему я вижу эту страницу?
404 означает, что файл не найден. Если вы уже загрузили файл, имя может быть написано с ошибкой или файл находится в другой папке.
Другие возможные причины
Вы можете получить ошибку 404 для изображений, поскольку у вас включена защита от горячих ссылок, а домен отсутствует в списке авторизованных доменов.
Если вы перейдете по временному URL-адресу (http://ip/~username/) и получите эту ошибку, возможно, проблема связана с набором правил, хранящимся в файле .htaccess. Вы можете попробовать переименовать этот файл в .htaccess-backup и обновить сайт, чтобы посмотреть, решит ли это проблему.
Также возможно, что вы непреднамеренно удалили корневую папку документа или ваша учетная запись должна быть создана заново. В любом случае, пожалуйста, немедленно свяжитесь с вашим веб-хостингом.
Вы используете WordPress? См. Раздел об ошибках 404 после перехода по ссылке в WordPress.
Как найти правильное написание и папку
Отсутствующие или поврежденные файлы
Когда вы получаете ошибку 404, обязательно проверьте URL-адрес, который вы пытаетесь использовать в своем браузере. Это сообщает серверу, какой ресурс он должен попытаться запросить.
http://example.com/example/Example/help.html
В этом примере файл должен находиться в папке public_html/example/Example/
Обратите внимание, что CaSe важен в этом примере. На платформах с учетом регистра e xample и E xample не совпадают.
На платформах с учетом регистра e xample и E xample не совпадают.
Для дополнительных доменов файл должен находиться в папке public_html/addondomain.com/example/Example/, а имена чувствительны к регистру.
Разбитое изображение
Если на вашем сайте отсутствует изображение, вы можете увидеть на своей странице поле с красным цветом X , где изображение отсутствует. Щелкните правой кнопкой мыши X и выберите «Свойства». Свойства сообщат вам путь и имя файла, который не может быть найден.
Это зависит от браузера. Если вы не видите на своей странице поле с красным X , попробуйте щелкнуть правой кнопкой мыши на странице, затем выберите «Просмотреть информацию о странице» и перейдите на вкладку «Мультимедиа».
http://example.com/cgi-sys/images/banner.PNG
В этом примере файл изображения должен находиться в папке public_html/cgi-sys/images/
Обратите внимание, что в этом примере важен CaSe . На платформах с учетом регистра символов PNG и png не совпадают.
На платформах с учетом регистра символов PNG и png не совпадают.
404 Ошибки после перехода по ссылкам WordPress
При работе с WordPress часто могут возникать ошибки 404 Page Not Found, когда была активирована новая тема или когда были изменены правила перезаписи в файле .htaccess.
Когда вы сталкиваетесь с ошибкой 404 в WordPress, у вас есть два варианта ее исправления.
Вариант 1: Исправьте постоянные ссылки
- Войдите в WordPress.
- В меню навигации слева в WordPress нажмите Настройки > Постоянные ссылки (Обратите внимание на текущую настройку. Если вы используете пользовательскую структуру, скопируйте или сохраните ее где-нибудь.)
- Выберите По умолчанию .
- Нажмите Сохранить настройки .
- Верните настройки к предыдущей конфигурации (до того, как вы выбрали «По умолчанию»). Верните пользовательскую структуру, если она у вас была.

- Нажмите Сохранить настройки .
Во многих случаях это сбросит постоянные ссылки и устранит проблему. Если это не сработает, вам может потребоваться отредактировать файл .htaccess напрямую.
Вариант 2. Измените файл .htaccess
Добавьте следующий фрагмент кода 9index.php$ — [L]
RewriteCond %{REQUEST_FILENAME} !-f
RewriteCond %{REQUEST_FILENAME} !-d
RewriteRule . /index.php [L]
# Конец WordPress
Если ваш блог показывает неправильное доменное имя в ссылках, перенаправляет на другой сайт или отсутствуют изображения и стиль, все это обычно связано с одной и той же проблемой: в вашем блоге WordPress настроено неправильное доменное имя.
Как изменить файл .htaccess
Файл .htaccess содержит директивы (инструкции), которые сообщают серверу, как вести себя в определенных сценариях, и напрямую влияют на работу вашего веб-сайта.
Перенаправление и переписывание URL-адресов — это две очень распространенные директивы, которые можно найти в файле . htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
htaccess, и многие скрипты, такие как WordPress, Drupal, Joomla и Magento, добавляют директивы в .htaccess, чтобы эти скрипты могли работать.
Возможно, вам потребуется отредактировать файл .htaccess в какой-то момент по разным причинам. В этом разделе рассказывается, как редактировать файл в cPanel, но не о том, что может потребоваться изменить. (Возможно, вам потребуется обратиться к другим статьям и ресурсам для получения этой информации.)
Существует множество способов редактирования файла .htaccess
- Отредактируйте файл на своем компьютере и загрузите его на сервер через FTP
- Использовать режим редактирования программы FTP
- Используйте SSH и текстовый редактор
- Используйте файловый менеджер в cPanel
Самый простой способ редактирования файла .htaccess для большинства людей — через диспетчер файлов в cPanel.
Как редактировать файлы .htaccess в файловом менеджере cPanel
Прежде чем что-либо делать, рекомендуется сделать резервную копию вашего веб-сайта, чтобы вы могли вернуться к предыдущей версии, если что-то пойдет не так.
Откройте файловый менеджер
- Войдите в cPanel.
- В разделе «Файлы» щелкните значок «Диспетчер файлов ».
- Установите флажок для Корень документа для и выберите доменное имя, к которому вы хотите получить доступ, из раскрывающегося меню.
- Убедитесь, что установлен флажок Показать скрытые файлы (точечные файлы) «.
- Нажмите Перейти . Файловый менеджер откроется в новой вкладке или окне.
- Найдите файл .htaccess в списке файлов. Возможно, вам придется прокрутить, чтобы найти его.
Для редактирования файла .htaccess
- Щелкните правой кнопкой мыши файл .htaccess и выберите Редактировать код в меню. Кроме того, вы можете щелкнуть значок файла .htaccess, а затем Редактор кода Значок вверху страницы.
- Может появиться диалоговое окно с вопросом о кодировании.
 Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне. - При необходимости отредактируйте файл.
- Нажмите Сохранить изменения в правом верхнем углу, когда закончите. Изменения будут сохранены.
- Протестируйте свой веб-сайт, чтобы убедиться, что ваши изменения были успешно сохранены. Если нет, исправьте ошибку или вернитесь к предыдущей версии, пока ваш сайт снова не заработает.
- После завершения нажмите Закрыть , чтобы закрыть окно диспетчера файлов.
8.4: Парабола — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 15099
- OpenStax
- OpenStax
Цели обучения
- Графические параболы с вершинами в начале координат.

- Запишите уравнения парабол в стандартной форме.
- Параболы графа с вершинами не в начале координат.
- Решение прикладных задач на параболах.
А вы знали, что олимпийский огонь зажигают за несколько месяцев до начала игр? Церемониальный метод зажжения пламени такой же, как и в древние времена. Церемония проходит в храме Геры в Олимпии, Греция, и уходит своими корнями в греческую мифологию, отдавая дань уважения Прометею, который украл огонь у Зевса, чтобы раздать его всем людям. Одна из одиннадцати действующих жриц помещает факел в фокус параболического зеркала (рис. \(\PageIndex{1}\)), которое фокусирует солнечные лучи и зажигает пламя.
Рисунок \(\PageIndex{1}\): Олимпийский факел завершает свое кругосветное путешествие, когда от него зажигают олимпийский котел во время церемонии открытия. (Источник: Кен Хэкман, ВВС США)
Параболические зеркала (или отражатели) способны улавливать энергию и фокусировать ее в одной точке. О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые тарелки, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары, и это лишь некоторые из них. Параболические отражатели также используются в устройствах альтернативной энергии, таких как солнечные плиты и водонагреватели, потому что они недороги в производстве и не требуют особого обслуживания. В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
О преимуществах этого свойства свидетельствует обширный список параболических объектов, которые мы используем каждый день: спутниковые тарелки, подвесные мосты, телескопы, микрофоны, прожекторы и автомобильные фары, и это лишь некоторые из них. Параболические отражатели также используются в устройствах альтернативной энергии, таких как солнечные плиты и водонагреватели, потому что они недороги в производстве и не требуют особого обслуживания. В этом разделе мы рассмотрим параболу и ее использование, в том числе недорогие и энергоэффективные солнечные конструкции.
Графическое изображение парабол с вершинами в начале координат
Ранее мы видели, что эллипс образуется, когда плоскость пересекает прямой круговой конус. Если плоскость параллельна ребру конуса, образуется неограниченная кривая. Эта кривая представляет собой параболу 90×107 90×108 (рис. \(\PageIndex{2}\)).
Рисунок \(\PageIndex{2}\): Парабола
Подобно эллипсу и гиперболе, парабола также может быть определена набором точек на координатной плоскости.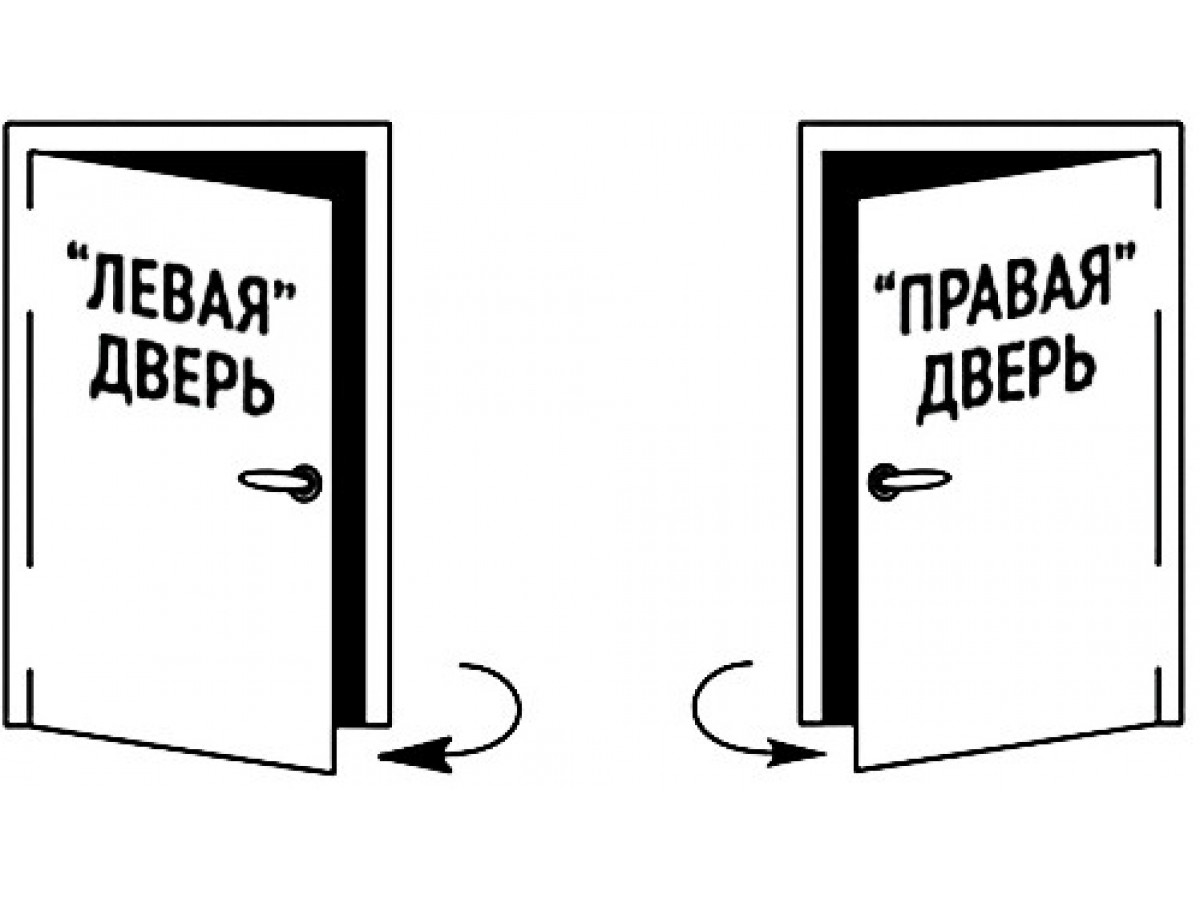 Парабола — это множество всех точек \((x,y)\) на плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой директриса , а фиксированная точка ( фокус ) не на директрисе.
Парабола — это множество всех точек \((x,y)\) на плоскости, которые находятся на одинаковом расстоянии от фиксированной линии, называемой директриса , а фиксированная точка ( фокус ) не на директрисе.
Ранее мы узнали о вершине параболы и оси симметрии. Теперь мы расширим обсуждение, включив в него другие ключевые свойства параболы (рис. \(\PageIndex{3}\)). Обратите внимание, что ось симметрии проходит через фокус и вершину и перпендикулярна директрисе. Вершина — это середина между директрисой и фокусом. Отрезок, проходящий через фокус и параллельный директрисе, называется 9-м.0107 широкая прямая кишка . Концы широкой прямой кишки лежат на кривой. По определению расстояние d от фокуса до любой точки \(P\) на параболе равно расстоянию от \(P\) до директрисы.
Рисунок \(\PageIndex{3}\): Основные характеристики параболы
Для работы с параболами в координатной плоскости мы рассмотрим два случая: с вершиной в начале координат и с вершиной в точке, отличной от начала координат.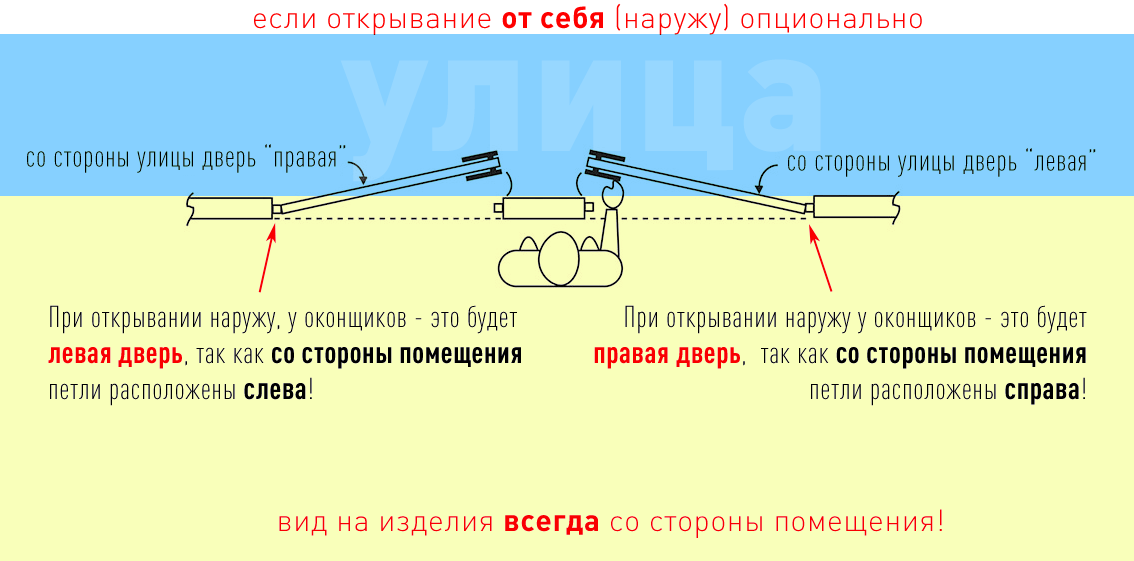 Начнем с первого.
Начнем с первого.
Рисунок \(\PageIndex{4}\) 92=4py\) когда ось y является осью симметрии. Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((0,0)\)
Таблица \(\PageIndex{1}\) и рисунок \(\PageIndex{5}\) суммируют стандартные характеристики парабол с вершиной в начале координат.
| Ось симметрии | \((0, р)\) | \(у=-р\) | \((\pm 2p, p)\) |
|---|
Рисунок \(\PageIndex{5}\): (a) Когда \(p>0\) и осью симметрии является ось x, парабола открывается вправо. (b) Когда \(p<0\) и осью симметрии является ось x, парабола открывается влево. (c) Когда \(p<0\) и осью симметрии является ось y, парабола раскрывается. (d) Когда \(p<0\) и осью симметрии является ось y, парабола открывается вниз.
(c) Когда \(p<0\) и осью симметрии является ось y, парабола раскрывается. (d) Когда \(p<0\) и осью симметрии является ось y, парабола открывается вниз.
Ключевыми характеристиками параболы являются ее вершина, ось симметрии, фокус, директриса и широкая прямая кишка (рис. \(\PageIndex{5}\)). Получив стандартное уравнение для параболы с центром в начале координат, мы можем легко определить ключевые особенности для построения графика параболы. Прямая называется касательной к кривой, если она пересекает кривую ровно в одной точке. Если мы нарисуем линии, касающиеся параболы в конечных точках прямой кишки , эти линии пересекутся на оси симметрии, как показано на рисунке \(\PageIndex{6}\). 92=4px\), тогда
- осью симметрии является ось \(x\), \(y=0\)
- набор \(4p\) равный коэффициенту \(x\) в данном уравнении для решения для \(p\). Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево.
- используйте \(p\) для нахождения координат фокуса, \((p,0)\)
- используйте \(p\) для нахождения уравнения направляющей, \(x=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((p,\pm 2p)\).
 В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда
В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда- осью симметрии является ось \(y\), \(x=0\)
- набор \(4p\) равный коэффициенту \(y\) в данном уравнении, которое нужно решить для \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(p\) для нахождения координат фокуса, \((0,p)\)
- используйте \(p\) для нахождения уравнения направляющей, \(y=−p\)
- используйте \(p\) для нахождения концов широкой прямой кишки, \((\pm 2p,p)\) 92=4px\). Таким образом, осью симметрии является ось x . Отсюда следует, что:
- \(24=4p\), значит \(p=6\). Так как \(p>0\), парабола выходит вправо
- координаты фокуса \((p,0)=(6,0)\)
- уравнение направляющей \(x=−p=−6\)
- конечные точки широкой прямой кишки имеют в фокусе одну и ту же координату x .
 Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\)
Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\)
92=4py\). Таким образом, осью симметрии является ось \(у\). Отсюда следует, что:
- \(−6=4p\), поэтому \(p=−\dfrac{3}{2}\). Так как \(p<0\), парабола направлена вниз.
- координаты фокуса равны \((0,p)=(0,−\dfrac{3}{2})\)
- уравнение направляющей \(y=−p=\dfrac{3}{2}\)
- конечные точки широкой прямой кишки можно найти, подставив \(y=\dfrac{3}{2}\) в исходное уравнение, \((\pm 3,−\dfrac{3}{2})\)
Далее наносим фокус, директрису и 92=8у\). Определите и обозначьте фокус, направляющую и конечные точки широкой прямой кишки .
- Ответить
- Фокус: \((0,2)\)
- Директриса: \(y=−2\)
- Конечные точки широкой прямой кишки: \((\pm 4,2)\).
Рисунок \(\PageIndex{10}\)
Написание уравнений параболы в стандартной форме
В предыдущих примерах мы использовали уравнение стандартной формы параболы для вычисления расположения ее ключевых элементов.
 2=4p(y−k)\) для парабол, у которых имеют ось симметрии, параллельную оси \(y\). Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
2=4p(y−k)\) для парабол, у которых имеют ось симметрии, параллельную оси \(y\). Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.СТАНДАРТНЫЕ ФОРМЫ ПАРАБОЛ С ВЕРШИНОЙ \((H, K)\)
Таблица \(\PageIndex{2}\) и рисунок \(\PageIndex{11}\) суммируют стандартные характеристики парабол с вершиной в точке \((h,k)\).
Таблица \(\PageIndex{2}\) Ось симметрии Уравнение Фокус Директриса Конечные точки широкой прямой кишки 92=4р(у-к)\) \((ч, к+р)\) \(у=к-р\) \((ч\пм 2р, к+р)\) Рисунок \(\PageIndex{11}\): (a) Когда \(p>0\), парабола открывается вправо.
 2=4p(y−k)\). 92=4p(x−h)\), тогда:
2=4p(y−k)\). 92=4p(x−h)\), тогда:- используйте данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(k\) для определения оси симметрии, \(y=k\)
- набор \(4p\) равный коэффициенту \((x−h)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола выходит вправо. Если \(p<0\), парабола открывается влево.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h+p, k)\) 92=4p(y−k)\), тогда:
- использовать данное уравнение для определения \(h\) и \(k\) для вершины, \((h,k)\)
- использовать значение \(h\) для определения оси симметрии, \(x=h\)
- набор \(4p\) равный коэффициенту \((y−k)\) в данном уравнении для решения \(p\). Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз.
- используйте \(h\), \(k\) и \(p\) , чтобы найти координаты фокуса, \((h, k+p)\)
- используйте \(k\) и \(p\) для нахождения уравнения направляющей, \(y=k−p\)
- используйте \(h\), \(k\) и \(p\) , чтобы найти концы широкой прямой кишки, \((h\pm 2p, k+p)\)
- Постройте вершину, ось симметрии, фокус, директрису и прямую кишку, а затем нарисуйте плавную кривую, чтобы сформировать параболу.

- вершина равна \((h,k)=(−3,1)\)
- ось симметрии \(y=k=1\)
- \(−16=4p\), поэтому \(p=−4\). Так как \(p<0\), парабола открывается влево.
- координаты фокуса равны \((h+p,k)=(−3+(−4),1)=(−7,1)\)
- уравнение направляющей \(x=h−p=−3−(−4)=1\)
- концами широкой прямой кишки являются \((h+p,k\pm 2p)=(−3+(−4),1\pm 2(−4))\), или \((−7,−7)\) и \((−7,92=4(х-8)\). Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((8,−1)\)
- Ось симметрии: \(y=−1\)
- Фокус: \((9,−1)\)
- Директриса: \(x=7\)
- Концы широкой прямой кишки : \((9,−3)\) и \((9,1)\).

Рисунок \(\PageIndex{13}\)
- вершина равна \((h,k)=(4,−8)\)
- ось симметрии \(x=h=4\)
- так как \(p=7\), \(p>0\) и таким образом парабола раскрывается
- координаты фокуса равны \((h,k+p)=(4,−8+7)=(4,−1)\)
- уравнение направляющей равно \(y=k−p=−8−7=−15\)
- концы широкой прямой кишки равны \((h\pm 2p,k+p)=(4\pm 2(7),−8+7)\), или \((−10,−1)\) и \((18,−1)\) 92=−20(y−3)\). Определите и обозначьте вершину, ось симметрии, фокус, направляющую и конечные точки прямой кишки latus .
- Ответить
- Вершина: \((−2,3)\)
- Ось симметрии: \(x=−2\)
- Фокус: \((−2,−2)\)
- Директриса: \(y=8\)
- Конечные точки широкой прямой кишки : \((−12,−2)\) и \((8,−2)\).
Рисунок \(\PageIndex{15}\)
Решение прикладных задач с использованием парабол
Как мы упоминали в начале раздела, параболы используются для проектирования многих объектов, которые мы используем каждый день, таких как телескопы, подвесные мосты, микрофоны и радиолокационное оборудование.
 Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.Рисунок \(\PageIndex{16}\): Отражающее свойство парабол
Параболические зеркала способны фокусировать солнечную энергию в одной точке, повышая температуру на сотни градусов за считанные секунды. Таким образом, параболические зеркала используются во многих недорогих, энергоэффективных солнечных продуктах, таких как солнечные плиты, солнечные обогреватели и даже дорожные разжигатели огня.
Пример \(\PageIndex{6}\): решение прикладных задач, связанных с параболами
На рисунке \(\PageIndex{17}\) показано поперечное сечение конструкции переносного солнечного пожарного пускового устройства.
 2=4py\),где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Замените } 2.25 \text{ на } x\\ y&\ приблизительно 0.74\qquad \text{Решите для } y \end{align*}\]
2=4py\),где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Замените } 2.25 \text{ на } x\\ y&\ приблизительно 0.74\qquad \text{Решите для } y \end{align*}\]Глубина тарелки примерно \(0,74\) дюймов.
Упражнение \(\PageIndex{6}\)
Солнечные плиты размером с балкон были разработаны для семей, живущих в Индии. Верх блюда имеет диаметр \(1600\) мм. Солнечные лучи отражаются от параболического зеркала в сторону «варки», расположенной \(320\) мм от основания.
- Найдите уравнение, моделирующее поперечное сечение солнечной плиты. Предположим, что вершина параболического зеркала является началом координатной плоскости и что парабола выходит вправо (т. е. имеет 92=4р(у-к)\)
Ключевые понятия
- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной линии, называемой директрисой, и фиксированной точки (фокуса), не лежащей на директрисе.

- Стандартная форма параболы с вершиной \((0,0)\) и осью x в качестве оси симметрии может быть использована для построения графика параболы. Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{1}\).
- Стандартная форма параболы с вершиной \((0,0)\) и осью y в качестве оси симметрии может быть использована для построения графика параболы. Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{2}\).
- Зная фокус и направляющую параболы, мы можем записать ее уравнение в стандартной форме. См. пример \(\PageIndex{3}\).
- Для построения параболы можно использовать стандартную форму параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(x\). Если \(p>0\), парабола открывается вправо. Если \(p<0\), парабола открывается влево. См. пример \(\PageIndex{4}\).
- Стандартная форма параболы с вершиной \((h,k)\) и осью симметрии, параллельной оси \(y\) может быть использована для построения параболы.
 Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).
Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\). - Реальные ситуации можно моделировать с помощью стандартных уравнений парабол. Например, зная диаметр и фокус поперечного сечения параболического отражателя, мы можем найти уравнение, моделирующее его стороны. См. пример \(\PageIndex{6}\).
Эта страница под названием 8.4: Парабола распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа ООР или издатель
- ОпенСтакс
- Показать страницу TOC
- нет
- Включено
- да
- Метки
- широкая прямая кишка
- парабола
- Парабола с горизонтальной осью
- Парабола с вертикальной осью
- источник@https://openstax.

- Парабола — это множество всех точек \((x,y)\) на плоскости, находящихся на одинаковом расстоянии от фиксированной линии, называемой директрисой, и фиксированной точки (фокуса), не лежащей на директрисе.
92&= 4⋅7⋅(y+8) \end{align*}\]
Отсюда следует, что:
Пример \(\PageIndex{4}\): построение параболы с вершиной \((h, k)\) и осью симметрии, параллельной оси \(x\) 92=4p(x−h)\). Таким образом, ось симметрии параллельна оси \(х\). Отсюда следует, что:
 – 2021.
– 2021.
 Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
Просто нажмите Изменить , чтобы продолжить. Редактор откроется в новом окне.
 В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда
В качестве альтернативы подставьте \(x=p\) в исходное уравнение. 92=4py\), тогда Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\)
Чтобы найти конечные точки, подставьте \(x=6\) в исходное уравнение: \((6,\pm 12)\) 2=4p(y−k)\) для парабол, у которых имеют ось симметрии, параллельную оси \(y\). Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.
2=4p(y−k)\) для парабол, у которых имеют ось симметрии, параллельную оси \(y\). Эти стандартные формы приведены ниже вместе с их общими графиками и ключевыми характеристиками.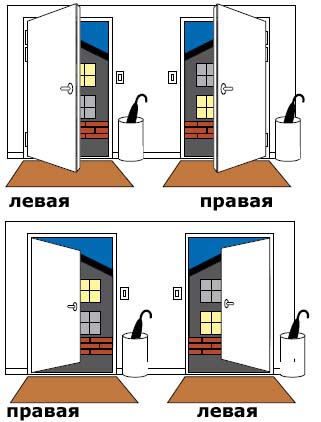 2=4p(y−k)\). 92=4p(x−h)\), тогда:
2=4p(y−k)\). 92=4p(x−h)\), тогда: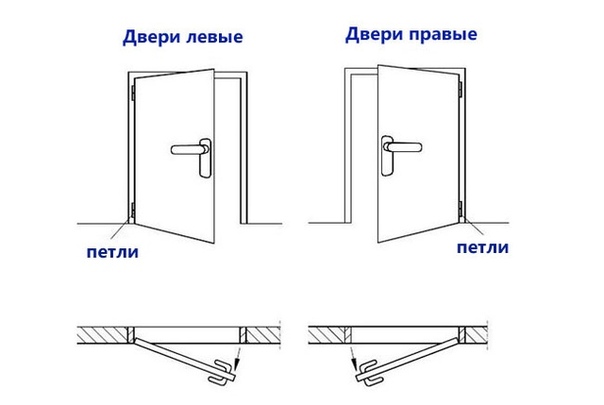

 Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.
Параболические зеркала, такие как то, которое использовалось для зажигания олимпийского огня, обладают уникальными отражающими свойствами. Когда лучи света, параллельные оси симметрии параболы, направляются на любую поверхность зеркала, свет отражается прямо в фокус (рис. \(\PageIndex{16}\)). Вот почему олимпийский факел зажигается, когда его держат в фокусе параболического зеркала.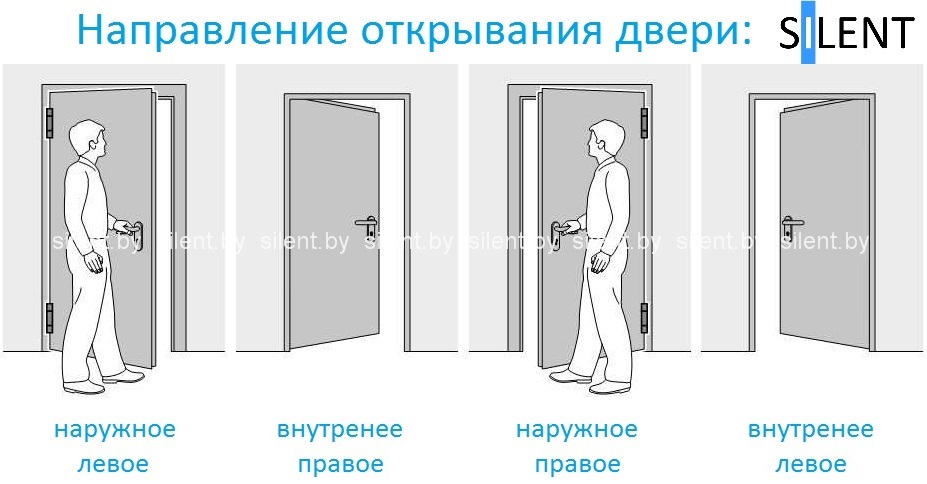 2=4py\),где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Замените } 2.25 \text{ на } x\\ y&\ приблизительно 0.74\qquad \text{Решите для } y \end{align*}\]
2=4py\),где \(p>0\). Воспламенитель, который является фокусом, находится на \(1,7\) дюймах выше вершины тарелки. Таким образом, мы имеем \(p=1,7\). 92&=6.8y\qquad \text{Замените } 2.25 \text{ на } x\\ y&\ приблизительно 0.74\qquad \text{Решите для } y \end{align*}\]
 Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).
Если \(p>0\), парабола раскрывается. Если \(p<0\), парабола раскрывается вниз. См. пример \(\PageIndex{5}\).