Пенополистирол ППС (пенопласт): цены, параметры

ППС (ПСБ С) – листовой утеплитель из пенополистирола со специальной добавкой — антипирен. Экологически чистый звуко- и теплоизоляционный материал выполненный в виде панелей, имеющий класс горючести (Г3). Самозатухающий пенополистирол ПСБ С (ППС) разрешен к применению в жилых и офисных зданиях. В соответствии с новым ГОСТом в маркировке плит ППС указываются цифры обозначающие минимально допустимую плотность для каждой марки.

Особенности утеплителей на основе пенополистирола

Водопоглощение

Пенополистирол поглощает воду при непосредственном контакте. Водопоглощение утеплителя зависит от его плотности, структурных особенностей, технологии изготовления и длительности контакта с влагой. Проникновение воды составляет менее 0,021 мм в месяц.

Паропроницаемость

Паропроницаемость пенополистирола не зависит от плотности и степени вспенивания. Величина имеет постоянно низкое значение 0,05 мг/(м*ч*Па).

Биологическая устойчивость

Пенополистирол состоит из углеводородов, не является питательной средой для грызунов и других живых организмов. В принудительных условиях грызуны могут воздействовать на утеплитель если он является препятствием/преградой для доступа к воде и пище или для удовлетворения других физиологических потребностей.

Долговечность

Долговечность утеплителей из пенополистирола составляет не менее 60 лет.

Пожаробезопасность

Пенополистирол при наличии в составе компонента — антипирена относится к самозатухающим материалам. Имеет класс горючести Г3. Снижение горючести пенополистирола также достигается при использовании для «надувания» гранул материала углекислого газа.

При выборе пенополистирола (пенопласта) в качестве утеплителя следует учитывать что материал с высокой плотностью будет обладать меньшими теплоизоляционным свойствам. Теплоизоляция из пенопласта, с низкой плотностью и прочностью, нуждается в максимальной защите от механического воздействия. Даже плотный утеплитель требует дополнительной защиты.

Области применения

Пенополистирол наиболее часто используется как конструкционный и теплоизоляционный материал.

В строительстве пенополистиров используют при утеплении:

Технические характеристики утеплителей из пенополистирола

• Плотность – 8-35 кг/м³





• Коэффициент теплопроводности – 0,038-0,046 Вт/м·К





• Водопоглощение – 1,8-3%





• Прочность на сжатие при деформации 10% – от 50 до 250 кПа





• Группа горючести – Г3

Особенности монтажа пенополистирола (пенопласта) на различные элементы конструкций

• Пенополистирол для пола выкладывают на черновой пол с последующей финишной стяжкой. Для этих работ используют утеплитель толщиной в 50 мм и плотностью 25-35 кг/м³. При утеплении деревянного пола изоляцию укладывают под лаги.




• Пенополистирол для стен покрывают армирующей сеткой и штукатуркой




• Пенополистирол для крыши монтируется двумя способами: первый — покрытие утеплителем толщиной 70 мм и заливка битумом; второй — холодная (вентилируемая) кровля, когда плиты теплоизоляции крепятся на тыльной стороне кровли




• Оптимальная толщина пенополистирола при утеплении фасада — 50-60 мм. Монтаж теплоизоляции происходит на заранее подготовленные и выровненные стены методом приклеивания и крепления дюбелями с последующим оштукатуриванием. Применяемый фасадные марки пенополистирола имееют плотность не менее 16 кг/м³ обозначаются литерой «Ф».

Примеры утепления пенопластом

Утепление фундаментаУтепление фасадаУтепление кровли

Полезное

Европейский опыт использования пенополистирола в пассивных домах

У нас вы можете купить утеплители ПСБ С (ППС) пенополистирол (пенопласт) по ценам приведенным выше. На странице каждого материала в указана стоимость с самовывозом со склада.

ППС, ПСБ-С: разбираемся в тонкостях маркировки пенополистирола | ГК Стройресурс

Начнем, как говорится, сначала. Сам термин “пенопласт” никогда не применяется в строительных нормативах и документах, единственно правильное название привычного материала — пенополистирол. Это разговорное и привычное многим название, которое давно уже вошло в обиход. Своему “правильному имени” он обязан вспенивающимся гранулам пенополистирола, из которых изготавливается.

В связи с тем, что несколько лет назад были полностью переработаны государственные стандарты по производству и маркировки пенопласта, у некоторых наших клиентов возникают вопрос: “Какой пенопласт выбрать?”.

Чем отличается ППС от ПСБ-С?

На самом деле ничем, если говорить конкретно о материале. И та, и другая маркировка указывают на то, что это привычный всем нам пенополистирол белого цвета.

ПСБ-С — это старая маркировка пенополистирола: ПС— пенополистирол, Б — беспрессованный метод производства, С — самозатухающийся.

ППС —ПеноПолиСтирол, так пенопласт маркируется по новым правилам.

В чем разница и зачем были заведены новые ГОСТы?

В маркировке пенопласта после букв ППС или ПСБ-С идут цифры, например ППС 25 или ПСБ-С 25.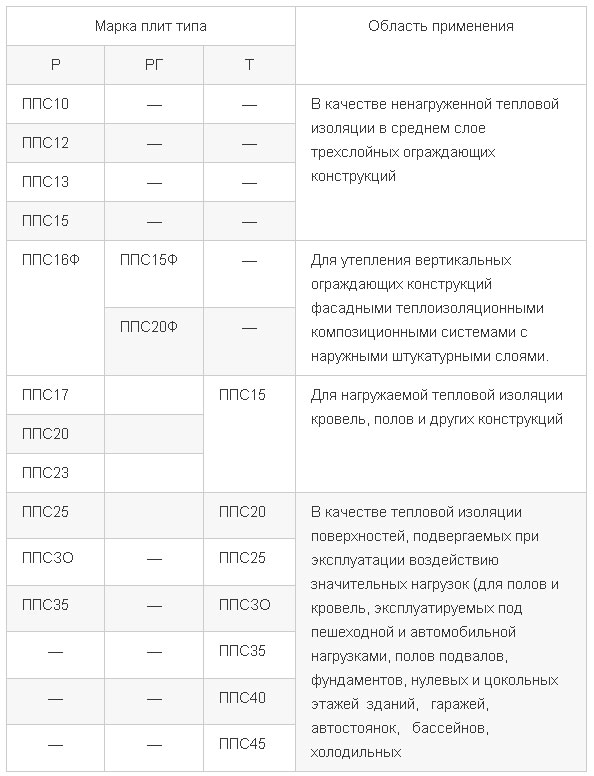 Эти числовые значения указывают на плотность материала. Отличие старой маркировки от новой заключается в том, что по предыдущим стандартам были разрешены отклонения от значения на 10 кг/м3.

Например, фактическая плотность пенопласта ПСБ-С 25 могла быть и чаще всего бывала не 25 кг/м3, а 15-16 кг/м3. Такая маркировка создавала путаницу, а потребитель легко мог ошибиться при выборе материала. По актуальному ГОСТу фактическая плотность материала должна полностью соответствовать маркировке.

Что обозначает буква “Ф” в маркировке пенополистирола, например, ППС 16 Ф?

Пенополистирол — один из самых популярных материалов для утепления декоративных штукатурных фасадов. Пенопласт недорогой, легкий, удобный в монтаже, долговечный и надежный материал. Для утепления штукатурных фасадов минимальная плотность пенополистирола должна быть 16 кг/м3, но это не единственная характеристика, которая имеет значение. Требования к утеплителю для штукатурных фасадов выше, чем для других конструкций, чтобы им соответствовать производители используют специальные добавки при изготовлении материала.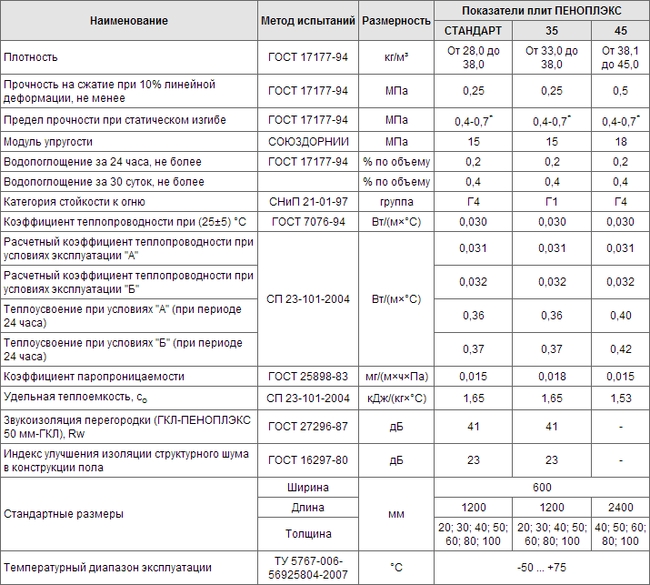

Роль специальных добавок в фасадный пенопласт:

✓ Снижают время самостоятельного горения: у обычного пенополистирола это 4 секунды, а у фасадного 1 секунда.

✓ Повышают прочность на сжатие на 15% в сравнении с аналогичным обычным пенополистиролом той же плотности

✓ Уменьшают водопоглощение с 4% до 1%.

Такой материал и маркируют с буквой “Ф”. Если Вам нужен пенополистирол для системы тонкослойного штукатурного фасада, то оптимальное решение с современной маркировкой — это ППС 16 Ф, который производится в разных толщинах от 20 мм, а стандартный размер листа 1000 х 1000 мм.

Что такое ЭППС?

Маркировка ЭППС не имеет прямого отношения к пенополистиролу, так обозначается экструдированный пенополистирол. Это абсолютно другой материал, который объединяет с пенопластом только сырье для производства. Сам же процесс изготовления, как и характеристики материала, принципиально другие. Экструдированный пенополистирол также часто сокращенно называют ХПС или XPS, это современный вид теплоизоляции с очень низкими показателями по влагопоглощению и теплопроводности.

Подробнее про экструдированный пенополистирол Вы можете прочитать в другой нашей статье: Экструдированный пенополистирол: преимущества, характеристики, область применения

density.ppp function — RDocumentation

Описание

Вычисление сглаженной ядром функции интенсивности по точечному образцу.

Использование

 # Метод S3 для ppp
плотность (x, сигма = NULL, …,
        веса = NULL, край = TRUE, varcov = NULL,
        at="пиксели", leaveoneout=TRUE,
        настроить = 1, копать = ЛОЖЬ, se = ЛОЖЬ,
        ядро = "гаусс",
        scalekernel=is.character(ядро),
        положительный=ЛОЖЬ, подробный=ИСТИНА) 

Аргументы

x

Точечный узор (объект класса "ppp" ).

сигма

Стандартное отклонение ядра изотропного сглаживания.
Либо числовое значение, либо функция, вычисляющая
соответствующее значение сигма .

грузы

Дополнительные грузы для крепления к точкам.
Числовой вектор, числовая матрица, выражение ,
или изображение в пикселях.

…

Дополнительные аргументы переданы в pixellate.ppp
и as.mask для определения
разрешение в пикселях или передается сигма , если это функция.

край

Логическое значение, указывающее, следует ли применять коррекцию края.

varcov

Дисперсионно-ковариационная матрица ядра анизотропного сглаживания.
Несовместим с сигма .

at

Строка, указывающая, следует ли вычислять значения интенсивности
в сетке местоположений пикселей ( at="pixels" ) или
только в точках x ( at="points" ).

leaveoneout

Логическое значение, указывающее, следует ли вычислять исключение
оценщик. Применимо только при at="points" .

регулировка

Дополнительно. Поправочный коэффициент для параметра сглаживания.

диггл

Логический. Если TRUE , используйте улучшенную коррекцию краев Джонса-Диггла,
который является более точным, но медленнее вычисляется, чем по умолчанию
коррекция.

ядро ​​

Сглаживающее ядро.
Строка символов, определяющая ядро ​​сглаживания.
(актуальные варианты "гауссов" , "епанечников" ,
"квартика" или "диск" ),
или изображение в пикселях (объект класса "im" )
содержащие значения ядра, или функцию (x, y) , которая
дает значения ядра.

масштабное ядро ​​

Логическое значение.
Если scalekernel=TRUE , то ядро ​​будет перемасштабировано.
пропускной способности, определяемой сигма и варков :
это поведение по умолчанию, когда ядро ​​ является строкой символов.
Если scalekernel=FALSE , то sigma и varcov
будет игнорироваться: это поведение по умолчанию, когда ядро ​​ является
функцию или изображение в пикселях.

se

Логическое значение, указывающее, следует ли также вычислять стандартные ошибки.

положительный

Логическое значение, указывающее, следует ли принудительно изменять все значения плотности.
быть положительными числами. По умолчанию ЛОЖЬ .

verbose

Логическое значение, указывающее, следует ли выдавать предупреждения
о числовых задачах и условиях.

Значение

По умолчанию результат
пиксельное изображение (объект класса "im" ).
Значения пикселей являются оценочными значениями интенсивности,
выражается в «очках на единицу площади».

Если at="points" , результатом будет числовой вектор
длины, равной количеству точек в x .
Значения являются оценочными значениями интенсивности в точках х .

В любом случае возвращаемое значение имеет атрибуты
"сигма" и "варков" которые сообщают о сглаживании
пропускная способность, которая использовалась.

Если весов является матрицей с более чем одним столбцом, то
результатом является список изображений (если at="pixels" ) или матрица
числовые значения (если at="points" ).

Если se=TRUE , результатом будет список с двумя элементами с именами
оценка и SE , каждый из описанных выше форматов.

Отрицательные значения

Возможны отрицательные и нулевые значения оценки плотности
когда at="pixels" из-за числовых ошибок конечной точности
арифметика.

По умолчанию density.ppp не пытается исправить такие ошибки.
Это потребует больше времени для вычислений и не всегда необходимо.
(Также было бы неуместно, если бы весов включали отрицательные значения.)

Чтобы результирующие значения плотности всегда были положительными,
установить положительное=ИСТИНА .

Детали

Это метод для общей функции плотности .

Вычисляет оценку ядра с фиксированной пропускной способностью.
(Diggle, 1985) функции интенсивности точечного процесса
который сгенерировал точечный шаблон x .

По умолчанию вычисляет свертку
изотропное ядро ​​Гаусса стандартного отклонения сигма
с точечными массами в каждой из точек данных в x .
Также поддерживаются анизотропные гауссовские ядра и негауссовские ядра.
Каждая точка имеет единичный вес, если только аргумент весит .
данный.

Если edge=TRUE , оценка интенсивности корректируется для
смещение краевого эффекта одним из двух способов:

• Если diggle=FALSE (по умолчанию), оценка интенсивности
  исправляется делением на свертки
  Ядро Гаусса с окном наблюдения.
  Это подход, первоначально описанный в Diggle (19).85).
  Таким образом, значение интенсивности в точке \(u\) равно
  $$
  \hat\lambda(u) = e(u) \sum_i k(x_i — u) w_i
  $$
  где \(к\) — ядро ​​сглаживания Гаусса,
  \(e(u)\) — краевой поправочный коэффициент,
  и \(w_i\) — веса.

• Если diggle=TRUE , код использует улучшенную коррекцию краев
  описан Джонсом (1993) и Дигглом (2010, уравнение 18.9).
  Было показано, что это дает лучшую производительность (Джонс, 1993).
  но вычисляется немного медленнее.
  Значение интенсивности в точке \(u\) равно
  $$
  \hat\lambda(u) = \sum_i k(x_i — u) w_i e(x_i)
  $$
  где снова \(к\) — ядро ​​сглаживания Гаусса,
  \(e(x_i)\) — поправочный коэффициент края,
  и \(w_i\) — веса.

В обоих случаях поправочный член \(e(u)\) является обратной величиной
масса ядра внутри окна:
$$
\ frac {1} {e (u)} = \ int_W k (vu) \, {\ rm d} v
$$
где \(W\) — окно наблюдения.

По умолчанию сглаживание выполняется с использованием ядра Гаусса,
с полосой сглаживания, определяемой аргументами
сигма , варков и настроить .

• , если сигма является одним числовым значением,
  это принято как стандартное отклонение изотропной гауссовой
  ядро.

• альтернативно сигма может быть функцией, которая вычисляет
  подходящая пропускная способность
  из шаблона точек данных, позвонив по номеру sigma(x) .
  Чтобы выполнить автоматический выбор пропускной способности с помощью перекрестной проверки,
  рекомендуется использовать функции
  чб.дигл ,
  бв.CvL ,
  ч. Скотт
  или
  бв.ппл .

• Сглаживающее ядро ​​может быть выполнено анизотропным
  давая ковариационно-дисперсионную матрицу 92, 2)) .

• , если не указан ни sigma , ни varcov ,
  будет использоваться изотропное ядро ​​Гаусса,
  со значением по умолчанию сигма
  рассчитывается по простому эмпирическому правилу
  это зависит только от размера окна.

• Аргумент настроить позволяет пользователю легко изменить
  пропускная способность, указанная любым из приведенных выше правил.
  Значение сигма будет умножено на
  фактор 92 . Чтобы удвоить пропускную способность сглаживания, установите
  настроить=2 .

• Бесконечная полоса пропускания, сигма=Inf или Adjust=Inf ,
  разрешено и дает оценку интенсивности, которая является постоянной
  над пространственной областью.

Выбор ядра сглаживания определяется аргументом ядро ​​ .
Это должна быть строка символов, задающая имя распознанного
двумерное ядро
(текущие варианты "гауссов" , "епанечников" ,
"квартика" или "диск" ),
или изображение в пикселях (объект класса "im" )
содержащие значения ядра, или функцию (x, y) , которая
дает значения ядра. По умолчанию используется ядро ​​Гаусса.

Если scalekernel=TRUE , то значения ядра будут перемасштабированы
по аргументам сигма , варков и
отрегулируйте , как описано выше, эффективно обрабатывая
9Ядро 0015 в качестве ядра шаблона со стандартным отклонением, равным 1.
Это поведение по умолчанию, когда ядро ​​ является строкой символов.
Если scalekernel=FALSE , значения ядра не будут изменены,
и аргументы sigma , varcov и настроить
игнорируются. Это поведение по умолчанию, когда ядро ​​ является
пиксельного изображения или функции.

Если at="pixels" (по умолчанию), значения интенсивности
вычисляется в каждом месте \(u\) в мелкой сетке,
и возвращаются в виде пиксельного изображения. Точечный шаблон сначала дискретизируется
используя pixellate.ppp , тогда интенсивность
вычисляется с помощью быстрого преобразования Фурье.
Точность зависит от разрешения в пикселях и правила дискретизации.
Разрешение в пикселях управляется аргументами
… передается на as.mask (указать количество
пикселей на dimyx или размер пикселя на eps ).
Правило дискретизации контролируется аргументами
… передано pixellate.ppp
(правило по умолчанию состоит в том, что каждая точка присваивается ближайшей
центр пикселя; это можно изменить с помощью аргументов
дробный и сохраняют ).

Если at="points" , вычисляются значения интенсивности
с высокой точностью только в точках x . Вычисление
выполняется путем прямой оценки и суммирования ядра
вклады без дискретизации данных. Результат — числовое
вектор, дающий значения плотности.
Значение интенсивности в точке \(x_i\) равно (если diggle=FALSE )
$$
\hat\lambda(x_i) = e(x_i) \sum_j k(x_j — x_i) w_j
$$
или (если копаться=ИСТИНА )
$$
\hat\lambda(x_i) = \sum_j k(x_j — x_i) w_j e(x_j)
$$
Если leaveoneout=TRUE (по умолчанию), то сумма в уравнении
берется по всем \(j\), не равным \(i\),
так, чтобы значение интенсивности на
точка данных представляет собой сумму вкладов ядра от
все другие точки данных.
Если leaveoneout=FALSE , то сумма берется по всем \(j\),
так что значение интенсивности в точке данных включает вклад
с той же точки.

Если весов является матрицей с более чем одним столбцом, то
вычисление эффективно повторяется для каждого столбца весов.
результатом является список изображений (если at="pixels" ) или матрица
числовые значения (если at="points" ).

Аргумент весов также может быть выражением .
Он будет оцениваться во фрейме данных как .data.frame(x) .
для получения вектора или матрицы весов. Выражение может включать
символы x и y представляют декартово
координаты, символ отмечает , представляющие значения меток
если имеется только один столбец оценок, а названия столбцов
отмечает, если столбцов несколько.

Аргумент веса также может быть пиксельным изображением
(объект класса «ИМ» ). числовые веса для точек данных
будут извлечены из этого изображения (просматривая значения пикселей
в местах точек данных в х ).

Для автоматического выбора полосы пропускания сигма с помощью
перекрестная проверка, использование
чб.дигл ,
бв.CvL ,
ч. Скотт
или
бв.ппл .

Для выполнения пространственной интерполяции значений, которые наблюдались
в точках точечного шаблона используйте Smooth.ppp .

Для адаптивной непараметрической оценки см.
адаптивная.плотность .
Для повышения резкости данных см. sharpen.ppp .

Чтобы вычислить поверхность относительного риска или карту вероятностей для
два (или более) типа точек, используйте relrisk .

Ссылки

Баддели, А., Рубак, Э. и Тернер, Р. (2015)
Образцы пространственных точек: методология и приложения с R .
Чепмен и Холл/CRC Press.

Диггл, Пи Джей (1985)
Метод ядра для сглаживания данных обработки точки.
Прикладная статистика (Журнал Королевского статистического общества,
Серия С) 34 (1985) 138—147.

Диггл, Пи Джей (2003)
Статистический анализ пространственных точечных структур ,
Второе издание. Арнольд.

Диггл, Пи Джей (2010)
Непараметрические методы.
Глава 18, стр. 299–316 в
А. Э. Гельфанд, П. Дж. Диггл, М. Фуэнтес и П. Гутторп (ред.)
Справочник по пространственной статистике ,
CRC Press, Бока-Ратон, Флорида.

Джонс, М.К. (1993)
Простые граничные поправки для оценки плотности ядра.
Статистика и вычисления 3 , 135—146.

См. также

bw.diggle ,
бв.CvL ,
ч. Скотт
bw.ppl для выбора пропускной способности.

Smooth.ppp ,
резкость.ppp ,
адаптивная плотность ,
повторный риск ,
ппп. 2)))
Z <- плотность (ячейки, 0,05, веса = data.frame (a = 1: 42, b = 42: 1)) Z <- плотность (ячейки, 0,05, веса = выражение (x)) # } # НЕ РАБОТАТЬ { # автоматический выбор пропускной способности график (плотность (ячейки, сигма = bw.diggle (ячейки)) # эквивалент: график (плотность (ячейки, ч.б.дигл)) # оценить интенсивность в точках плотность (ячейки, 0,05, в = "точки") график (плотность (ячейки, сигма = 0,4, ядро ​​​​=" епанечников")) # расчет относительного риска вручную (см. relrisk.ppp) легкое <- разделить (чорли) $ легкое гортань <- разделенная (хорли) $ гортань D <- плотность (легкие, сигма = 2) график (плотность (гортань, сигма = 2, веса = 1 / D)) # }

Запустите приведенный выше код в браузере с помощью DataCamp Workspace

Функцияdens.ppp — RDocumentation

Описание

Вычислите сглаженную ядром функцию интенсивности по точечному шаблону.

Использование

 # Метод S3 для ppp
плотность (x, сигма = NULL, …,
        веса = NULL, край = TRUE, varcov = NULL,
        at="пиксели", leaveoneout=TRUE,
        настроить = 1, копать = ЛОЖЬ, se = ЛОЖЬ,
        ядро = "гаусс",
        scalekernel=is. character(ядро),
        положительный=ЛОЖЬ, многословный=ИСТИНА) 

Аргументы

x

Точечный шаблон (объект класса "ppp" ).

сигма

Полоса сглаживания (степень сглаживания).
Стандартное отклонение ядра изотропного сглаживания.
Либо числовое значение,
или функция, которая вычисляет соответствующее значение sigma .

грузы

Дополнительные грузы для крепления к точкам.
Числовой вектор, числовая матрица, выражение ,
или изображение в пикселях.

…

Дополнительные аргументы переданы в pixellate.ppp
и as.mask для определения
разрешение в пикселях или передается сигма , если это функция.

край

Логическое значение, указывающее, следует ли применять коррекцию края.

varcov

Дисперсионно-ковариационная матрица ядра анизотропного сглаживания.
Несовместим с сигма .

at

Строка, указывающая, следует ли вычислять значения интенсивности
в сетке местоположений пикселей ( at="пиксели" ) или
только в точках x ( at="points" ).

leaveoneout

Логическое значение, указывающее, следует ли вычислять исключение
оценщик. Применимо только при at="points" .

регулировка

Дополнительно. Поправочный коэффициент для параметра сглаживания.

диггл

Логический. Если TRUE , используйте улучшенную коррекцию краев Джонса-Диггла,
который является более точным, но медленнее вычисляется, чем по умолчанию
коррекция.

ядро ​​

Сглаживающее ядро.
Строка символов, определяющая ядро ​​сглаживания.
(актуальные варианты "гауссов" , "епанечников" ,
"квартика" или "диск" ),
или изображение в пикселях (объект класса "im" )
содержащие значения ядра, или функцию (x, y) , которая
дает значения ядра.

масштабное ядро ​​

Логическое значение.
Если scalekernel=TRUE , то ядро ​​будет перемасштабировано.
пропускной способности, определяемой сигма и варков :
это поведение по умолчанию, когда ядро ​​ является строкой символов.
Если scalekernel=FALSE , то sigma и varcov
будет игнорироваться: это поведение по умолчанию, когда ядро ​​ является
функцию или изображение в пикселях.

se

Логическое значение, указывающее, следует ли также вычислять стандартные ошибки.

положительный

Логическое значение, указывающее, следует ли принудительно изменять все значения плотности.
быть положительными числами. По умолчанию ЛОЖЬ .

verbose

Логическое значение, указывающее, следует ли выдавать предупреждения
о числовых задачах и условиях.

Значение

По умолчанию результат
пиксельное изображение (объект класса "im" ).
Значения пикселей являются оценочными значениями интенсивности,
выражается в «очках на единицу площади».

Если at="points" , результатом будет числовой вектор
длины, равной количеству точек в x .
Значения являются оценочными значениями интенсивности в точках х .

В любом случае возвращаемое значение имеет атрибуты
"сигма" и "варков" которые сообщают о сглаживании
пропускная способность, которая использовалась.

Если весов является матрицей с более чем одним столбцом, то
результатом является список изображений (если at="pixels" ) или матрица
числовые значения (если at="points" ).

Если se=TRUE , результатом будет список с двумя элементами с именами
оценка и SE , каждый из описанных выше форматов.

Величина сглаживания

Величина сглаживания определяется аргументами
сигма , варков и настроить .

• , если сигма является одним числовым значением,
это принято как стандартное отклонение изотропной гауссовой
ядро.

• альтернативно сигма может быть функцией, которая вычисляет
подходящая пропускная способность
из шаблона точек данных, вызвав сигма(х) .
Чтобы выполнить автоматический выбор пропускной способности с помощью перекрестной проверки,
рекомендуется использовать функции
чб.дигл ,
бв.CvL ,
ч. Скотт
или
бв.ппл .

• Сглаживающее ядро ​​может быть выполнено анизотропным
задав матрицу дисперсии-ковариации varcov .
Аргументы sigma и varcov несовместимы.

• Альтернативно 92, 2)) .

• , если не указан ни sigma , ни varcov ,
  будет использоваться изотропное ядро ​​Гаусса,
  со значением по умолчанию сигма
  рассчитывается по простому эмпирическому правилу
  это зависит только от размера окна.

• Аргумент настроить позволяет пользователю легко изменить
  пропускная способность, указанная любым из приведенных выше правил.
  Значение сигма будет умножено на
  фактор 92 . Чтобы удвоить пропускную способность сглаживания, установите
  настроить=2 .

• Бесконечная полоса пропускания, сигма=Inf или Adjust=Inf ,
  разрешено и дает оценку интенсивности, которая является постоянной
  над пространственной областью.

Коррекция края

Если edge=TRUE , оценка интенсивности корректируется для
смещение краевого эффекта одним из двух способов:

• Если diggle=FALSE (по умолчанию), оценка интенсивности
  исправляется делением на свертки
  Ядро Гаусса с окном наблюдения.
  Это подход, первоначально описанный в Diggle (19).85).
  Таким образом, значение интенсивности в точке \(u\) равно
  $$
  \hat\lambda(u) = e(u) \sum_i k(x_i — u) w_i
  $$
  где \(к\) — ядро ​​сглаживания Гаусса,
  \(e(u)\) — краевой поправочный коэффициент,
  и \(w_i\) — веса.

• Если diggle=TRUE , код использует улучшенную коррекцию краев
  описан Джонсом (1993) и Дигглом (2010, уравнение 18.9).
  Было показано, что это дает лучшую производительность (Джонс, 1993).
  но вычисляется немного медленнее.
  Значение интенсивности в точке \(u\) равно
  $$
  \hat\lambda(u) = \sum_i k(x_i — u) w_i e(x_i)
  $$
  где снова \(к\) — ядро ​​сглаживания Гаусса,
  \(e(x_i)\) — поправочный коэффициент края,
  и \(w_i\) — веса.

В обоих случаях поправочный член \(e(u)\) является обратной величиной
масса ядра внутри окна:
$$
\ frac {1} {e (u)} = \ int_W k (vu) \, {\ rm d} v
$$
где \(W\) — окно наблюдения.

Ядро сглаживания

По умолчанию сглаживание выполняется с использованием ядра Гаусса.

Выбор ядра сглаживания определяется аргументом ядро ​​ .
Это должна быть строка символов, задающая имя распознанного
двумерное ядро
(текущие варианты "гауссов" , "епанечников" ,
"квартика" или "диск" ),
или изображение в пикселях (объект класса "im" )
содержащие значения ядра, или функцию (x, y) , которая
дает значения ядра. По умолчанию используется ядро ​​Гаусса.

Если scalekernel=TRUE , то значения ядра будут перемасштабированы
по аргументам сигма , варков и
отрегулируйте , как описано выше, эффективно обрабатывая
9Ядро 0015 в качестве ядра шаблона со стандартным отклонением, равным 1.
Это поведение по умолчанию, когда ядро ​​ является строкой символов.
Если scalekernel=FALSE , значения ядра не будут изменены,
и аргументы sigma , varcov и настроить
игнорируются. Это поведение по умолчанию, когда ядро ​​ является
пиксельного изображения или функции.

Желаемый результат

Если at="pixels" (по умолчанию), значения интенсивности
вычисляется в каждом месте \(u\) в мелкой сетке,
и возвращаются в виде пиксельного изображения. Точечный шаблон сначала дискретизируется
используя pixellate.ppp , тогда интенсивность
вычисляется с помощью быстрого преобразования Фурье.
Точность зависит от разрешения в пикселях и правила дискретизации.
Разрешение в пикселях управляется аргументами
… передается на as.mask (указать количество
пикселей на dimyx или размер пикселя на eps ).
Правило дискретизации контролируется аргументами
… передано pixellate.ppp
(правило по умолчанию состоит в том, что каждая точка присваивается ближайшей
центр пикселя; это можно изменить с помощью аргументов
дробный и сохраняют ).

Если at="points" , вычисляются значения интенсивности
с высокой точностью только в точках x . Вычисление
выполняется путем прямой оценки и суммирования ядра
вклады без дискретизации данных. Результат — числовое
вектор, дающий значения плотности.
Значение интенсивности в точке \(x_i\) равно (если diggle=FALSE )
$$
\hat\lambda(x_i) = e(x_i) \sum_j k(x_j — x_i) w_j
$$
или (если копаться=ИСТИНА )
$$
\hat\lambda(x_i) = \sum_j k(x_j — x_i) w_j e(x_j)
$$
Если leaveoneout=TRUE (по умолчанию), то сумма в уравнении
берется по всем \(j\), не равным \(i\),
так, чтобы значение интенсивности на
точка данных представляет собой сумму вкладов ядра от
все другие точки данных.
Если leaveoneout=FALSE , то сумма берется по всем \(j\),
так что значение интенсивности в точке данных включает вклад
с той же точки.

Веса

Если весов является матрицей с более чем одним столбцом, то
вычисление эффективно повторяется для каждого столбца весов.
результатом является список изображений (если at="pixels" ) или матрица
числовые значения (если at="points" ).

Аргумент весов также может быть выражением .
Он будет оцениваться во фрейме данных как .data.frame(x) .
для получения вектора или матрицы весов. Выражение может включать
символы x и y представляют декартово
координаты, символ отмечает , представляющие значения меток
если имеется только один столбец оценок, а названия столбцов
отмечает, если столбцов несколько.

Аргумент веса также может быть пиксельным изображением
(объект класса «ИМ» ). числовые веса для точек данных
будут извлечены из этого изображения (просматривая значения пикселей
в местах точек данных в х ).

Значение

density.ppp

Эту функцию часто неправильно понимают.

Результат density.ppp не является пространственным сглаживанием
меток или весов, прикрепленных к точечному шаблону.
Для выполнения пространственной интерполяции значений, которые наблюдались
в точках точечного шаблона используйте Smooth.ppp .

Результат density.ppp не является плотностью вероятности.
Это оценка функция интенсивности
точечный процесс, сгенерировавший данные точечного шаблона.
Интенсивность — это ожидаемое количество случайных точек
на единицу площади.
Единицами интенсивности являются «баллы на единицу площади».
Интенсивность обычно является функцией пространственного положения,
и именно эта функция оценивается плотностью .ppp .
Интеграл функции интенсивности по пространственной области дает
ожидаемое количество точек, попадающих в эту область.

Проверка оценки функции интенсивности обычно
первый шаг в изучении набора данных шаблона пространственных точек.
Дополнительные пояснения см. в Baddeley, Rubak and Turner (2015).
или Диггл (2003, 2010).

Если у вас есть два (или более) типа баллов, и вы хотите
карта вероятностей или поверхность относительного риска (изменяющаяся в пространстве
вероятность данного типа), используйте relrisk .

Техническая проблема: Отрицательные значения

Возможны отрицательные и нулевые значения оценки плотности
когда at="pixels" из-за числовых ошибок конечной точности
арифметика.

По умолчанию density.ppp не пытается исправить такие ошибки.
Это потребует больше времени для вычислений и не всегда необходимо.
(Также было бы неуместно, если бы веса включают отрицательные значения.)

Чтобы результирующие значения плотности всегда были положительными,
установить положительное=ИСТИНА .

Детали

Это метод для общей функции плотности .

Вычисляет оценку ядра с фиксированной пропускной способностью.
(Diggle, 1985) функции интенсивности точечного процесса
который сгенерировал точечный шаблон x .

Величина сглаживания контролируется сигмой
если он указан.

По умолчанию сглаживание выполняется с использованием ядра Гаусса.
Полученная оценка плотности является сверткой
изотропное ядро ​​Гаусса со стандартным отклонением сигма ,
с точечными массами в каждой из точек данных в x .

Также поддерживаются анизотропные и негауссовые ядра.
Каждая точка имеет единичный вес, если только аргумент весит .
данный.

Если край=ИСТИНА (по умолчанию), оценка интенсивности исправлена
для смещения краевого эффекта.

Если at="pixels" (по умолчанию), результатом будет изображение в пикселях.
давая предполагаемую интенсивность для каждого пикселя в сетке.
Если at="points" , результатом будет числовой вектор, дающий
предполагаемая интенсивность в каждой из исходных точек данных в x .

Ссылки

Баддели, А., Рубак, Э. и Тернер, Р. (2015)
Образцы пространственных точек: методология и приложения с R .
Чепмен и Холл/CRC Press.

Диггл, Пи Джей (1985)
Метод ядра для сглаживания данных обработки точки.
Прикладная статистика (Журнал Королевского статистического общества,
Серия С) 34 (1985) 138—147.

Диггл, Пи Джей (2003)
Статистический анализ пространственных точечных структур ,
Второе издание. Арнольд.

Диггл, Пи Джей (2010)
Непараметрические методы.
Глава 18, стр. 299–316 в
А. Э. Гельфанд, П. Дж. Диггл, М. Фуэнтес и П. Гутторп (ред.)
Справочник по пространственной статистике ,
CRC Press, Бока-Ратон, Флорида.

Джонс, М. К. (1993)
Простые граничные поправки для оценки плотности ядра.
Статистика и вычислительная техника 3 , 135–146.

См. также

Для автоматического выбора полосы пропускания сигма с помощью
перекрестная проверка, использование
чб.дигл ,
бв.CvL ,
ч. Скотт
или
бв.ппл .

Для выполнения пространственной интерполяции значений, которые наблюдались
в точках точечного шаблона используйте Smooth.ppp .

Для адаптивной непараметрической оценки см.
адаптивная.плотность .
Для увеличения резкости данных см. sharpen.ppp .

Чтобы вычислить поверхность относительного риска или карту вероятностей для
два (или более) типа точек, используйте relrisk .

Для получения информации о структурах данных см.
ппп.объект ,
им.объект .

Примеры

Запустить этот код

 # NOT RUN {
 если (интерактивный ()) {
 опа <- номинал (mfrow=c(1,2))
 график (плотность (ячейки, 0,05))
 график (плотность (ячейки, 0,05, диггл = ИСТИНА))
 пар(опа)
 v <- диаг (с (0,05, 0,07) ^ 2)
 график (плотность (ячейки, varcov = v))
 }
 # автоматический выбор пропускной способности
 график (плотность (ячейки, сигма = bw.