Коэффициент пропускания атмосферы: § 2.3. Пропускание атмосферы в спектральных интервалах
Пропускание излучения атмосферой | Системы тепловидения
- Подробности
- Категория: Разное-архив
- тепловизионный
Содержание материала
- Системы тепловидения
- Назначение систем тепловидения
- История систем тепловидения
- Основы получения теплового изображения
- Источники информации, пример системы
- Теория теплового излучения
- Пропускание излучения атмосферой
- Теория линейной фильтрации
- Сокращенная система обозначений в фурье-анализе
- Эквивалентная полоса частот
- Физиология зрительного восприятия
- Пространственно-частотная характеристика
- Чувствительность к частоте случайного шума
- Интегрирующие свойства глаза
- Влияние кадровой развертки на восприятие изображения
- Обнаружение объектов на фоне случайных шумов
- Субъективное восприятие резкости изображения
- Обобщенные критерии
- Минимальная разрешаемая разность температур
- Параметры эффективности работы
- Оптика
- Оптические материалы для тепловизионных систем
- Сканирующие устройства
- Вращающиеся преломляющие клинья
- Другие системы сканирования
- Эффекты затемнения
- Типы тепловизионных систем
- Эвапорографы и видиконы
- Инфракрасные квантовые счетчики
- Выборка
- Выборка в системах с коммутацией
- Визуальное восприятие объектов
- Разрешение эквивалентных штриховых мир
- Вероятность обнаружения и опознавания
- Эксперименты с обработкой на ЭВМ
- Другие ограничения при наблюдении
- Измерение характеристик систем
- Тепловые изображения
Страница 7 из 38
Фиг. 2.8. Радиационный контраст в диапазоне 8—14 мкм в зависимости ют разности температур объекта и фона для четырех значений температуры фона.
2.8. Радиационный контраст в диапазоне 8—14 мкм в зависимости ют разности температур объекта и фона для четырех значений температуры фона.
в широком спектральном диапазоне контрасты существенно меньше, чем в рассмотренных выше узких диапазонах. На этом мы закончим рассмотрение основных соотношений теории теплового излучения. Более подробную информацию можно найти в работах [1—9].
2.3, Пропускание излучения атмосферой
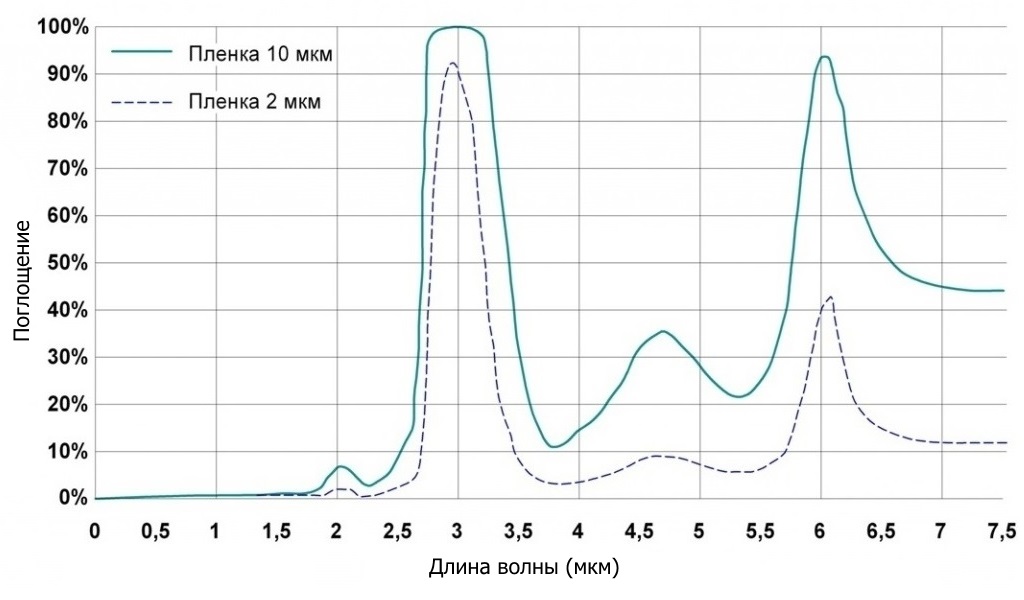
Тепловое излучение ослабляется при прохождении через земную атмосферу вследствие поглощения и рассеяния молекулами газа, скоплениями молекул (аэрозолями), дождем, снегом, а также дымом, туманом, дымкой, смогом. Следующие молекулы (перечисленные ниже в порядке важности) поглощают инфракрасное излучение в широких полосах с центрами, соответствующими указанным длинам волн: воды (2,7; 3,2; 6,3 мкм), углекислого газа (2,7;, 4,3; 15 мкм), озона (4,8; 9,6; 14,2 мкм), закиси азота (4,7; 7,8 мкм), окиси углерода (4,8 мкм) и метана (3,2; 7,8 мкм). Не считая ослабления в плотных дисперсных средах, молекулярное поглощение является главной причиной ослабления излучения, причем наиболее сильно излучение поглощается парами воды, углекислым газом и озоном.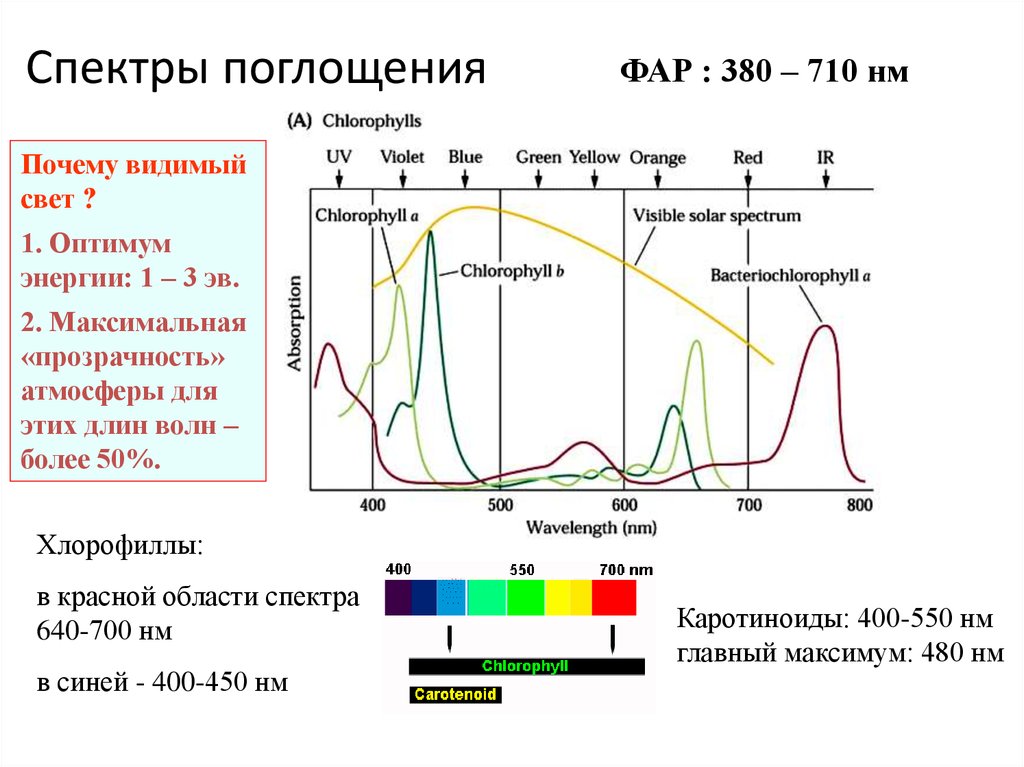 В нижних слоях атмосферы поглощением закисью азота и окисью углерода обычно можно пренебречь. Полосы поглощения водяного пара с центром 6,3 мкм и углекислого газа с центрами 2,7 и 15 мкм ограничивают пропускание излучения атмосферой в диапазоне длин волн 2—20 мкм, определяя положение двух окон прозрачности: 3,5—5 и 8—14 мкм.
В нижних слоях атмосферы поглощением закисью азота и окисью углерода обычно можно пренебречь. Полосы поглощения водяного пара с центром 6,3 мкм и углекислого газа с центрами 2,7 и 15 мкм ограничивают пропускание излучения атмосферой в диапазоне длин волн 2—20 мкм, определяя положение двух окон прозрачности: 3,5—5 и 8—14 мкм.
На данной длине волны при определенном состоянии атмосферы коэффициент пропускания атмосферы определяется законом Бугера — Ламберта — Бэра
Фиг. 2.10. Пропускание атмосферы в диапазоне длин волн 2,8—4,2 мкм [12].
1 — трасса 300 м, толщина слоя осажденной воды 0,11 см; 2 — трасса 6,3 км, толщина слоя осажденной воды 1,37 см; 3 — трасса 18,7 км, толщина слоя осажденной воды 5,2 см.
Фиг. 2.11. Пропускание атмосферы в диапазоне длин волн 4,3—5,6 мкм [12].
1 —трасса 300 м, толщина слоя осажденной воды 0,11 см; 2 — трасса 6,3 км, толщина слоя осажденной воды 1,37 см; 3 — трасса 18,7 км, толщина слоя осажденной воды 5,2 см.
Фиг. 2.12. Пропускание атмосферы в диапазоне длин волн 6,5—14 мкм [12].
- — трасса 300 м, толщина слоя осажденной воды 0,11 см; 2 — трасса 6,3 км, толщина слоя осажденной воды 1,37 см; 3—трасса 18,7 км, толщина слоя осажденной воды
- см.
Фиг. 2.6. Значения производной плотности потока излучения, соответствующей закону Планка, по температуре для диапазона 3,5—5 мкм в функции температуры фона.
Фиг. 2.13. Пропускание атмосферы в диапазоне длин волн 3—5 мкм [13].
Длина трассы 25 км; толщина слоя осажденной воды: 1 — 21,5 см; 2 — 25,4 см; з —
- см; 4 — 43,3 см.
Фиг. 2.14. Пропускание атмосферы в диапазоне длин волн 4,2—10,7 мкм [13]. Длина трассы 25 км; толщина слоя осажденной воды: 1 — 21,5 см; 2 — 26,7 см.
и мы их здесь рассматривать не будем. Просто мы воспользуемся наиболее подходящей из известных аналитических моделей.
Поглощение молекулами газа происходит в том случае, когда колебательные и вращательные движения атомов в молекуле вызывают изменение дипольного момента. При этом энергетическое взаимодействие молекулы с электромагнитным полем может проявляться в резонансном поглощении и испускании квантов. Следовательно, изолированным симметричным молекулам, не имеющим дипольного момента, не свойственно колебательно-вращательное поглощение. Молекулярное поглощение в электронных зонах атомов также пренебрежимо мало. По этим причинам изолированные молекулы трех основных компонентов атмосферы — двухатомные молекулы азота и кислорода и одноатомная молекула аргона — не поглощают инфракрасного излучения. В газе, однако, происходит уширение линий поглощения, вызванное давлением. Этот эффект соответствующим образом влияет на поглощение излучения в атмосфере.
При этом энергетическое взаимодействие молекулы с электромагнитным полем может проявляться в резонансном поглощении и испускании квантов. Следовательно, изолированным симметричным молекулам, не имеющим дипольного момента, не свойственно колебательно-вращательное поглощение. Молекулярное поглощение в электронных зонах атомов также пренебрежимо мало. По этим причинам изолированные молекулы трех основных компонентов атмосферы — двухатомные молекулы азота и кислорода и одноатомная молекула аргона — не поглощают инфракрасного излучения. В газе, однако, происходит уширение линий поглощения, вызванное давлением. Этот эффект соответствующим образом влияет на поглощение излучения в атмосфере.
Молекулярное поглощение ослабляет пучок теплового излучения, поскольку газ переизлучает поглощенную энергию во всех направлениях, а не только в направлении первоначального распространения. Четкое объяснение процесса молекулярного поглощения дается Эндингом [14]. В его работе приведено описание модели Эльзассера, статистической модели и модели Эльзассера со случайным наложением полос. Эндинг дает рекомендации по применению моделей к различным молекулярным компонентам и сравнивает результаты, полученные с помощью этих моделей, с экспериментальными данными. Молекулярное рассеяние и ослабление излучения на аэрозолях хорошо описаны в работе Макклэтчи и др. [10]. Монографии по инфракрасной технике содержат обобщающие сведения о моделях поглощения в одиночных линиях и полосах.
Эндинг дает рекомендации по применению моделей к различным молекулярным компонентам и сравнивает результаты, полученные с помощью этих моделей, с экспериментальными данными. Молекулярное рассеяние и ослабление излучения на аэрозолях хорошо описаны в работе Макклэтчи и др. [10]. Монографии по инфракрасной технике содержат обобщающие сведения о моделях поглощения в одиночных линиях и полосах.
При высокой относительной влажности молекулы паров воды собираются в скопления, образуя аэрозоль. Такое состояние атмосферы занимает промежуточное положение между влажной атмосферой и туманом или дымкой. Используя подходящие модели молекулярного поглощения и рассеяния, а также модель рассеяния на аэрозолях, Ходжес [15] сравнил расчетные и экспериментальные данные и выяснил, что при высокой относительной влажности ослабление практически полностью определяется поглощением на жидких аэрозолях. На небольших высотах и на умеренных расстояниях, когда концентрация паров воды мала, ослабление, по данным Ходжеса, определяется одним молекулярным поглощением.
Рассеяние молекулами, аэрозолями, туманом, дымкой и облаками можно объяснить с помощью теории Ми. Теория Ми справедлива для рассеяния на малых частицах, размер которых значительно меньше длины волны (рэлеевское рассеяние), и для рассеяния на больших частицах, размер которых значительно больше длины волны (неселективное рассеяние). Поскольку рэлеевское рассеяние происходит по закону Аг4, молекулярное рэлеевское рассеяние не играет существенной роли в области к > 2 мкм. В результате рассеяние на молекулах (р к) в этой области можно не учитывать по сравнению с поглощением; нужно принимать во внимание только рассеяние на скоплениях молекул.
Наиболее подробное рассмотрение всех источников ослабления излучения в атмосфере содержится в работе Макклэтчи и др. [10]. Их методы расчета ослабления в интервале длин волн 0,25—25 мкм основываются на следующих механизмах:
на молекулярном поглощении в отдельных линиях для всех, основных газов;
на молекулярном поглощении в уширенных давлением линиях паров воды;
на молекулярном рассеянии для всех компонентов атмосферы;
на ослаблении на аэрозолях всех типов.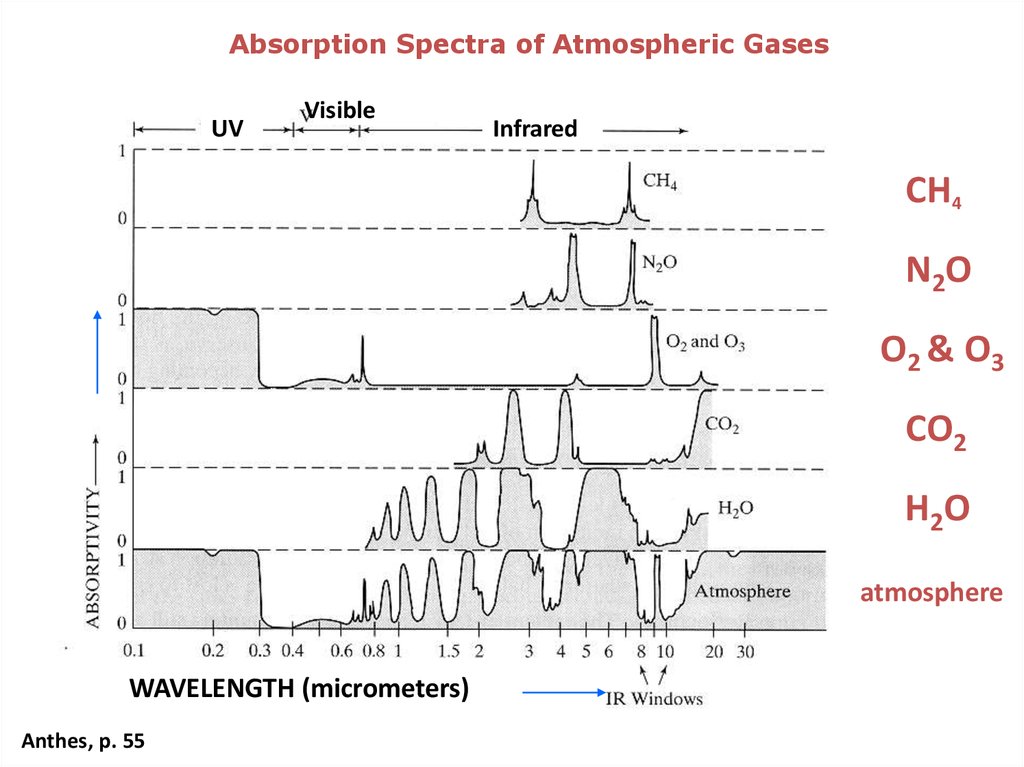
В работе [10] приведены также таблицы характеристик семи моделей атмосферы: тропические условия, лето и зима в средних широтах, субарктические зима и лето, условия чистой атмосферы (метеорологическая дальность видимости 23 км) и дымка (метеорологическая дальность видимости 5 км).
На фиг. 2.15—2.19 [10] приведены зависимости коэффициентов пропускания от длины волны для различных плотностей поглощающих компонентов или длины трассы для молекулярного поглощения в линиях паров воды, не уширенных давлением; для непрерывного спектра поглощения паров воды, уширенного давлением; для равномерно распределенной смеси газов; для молекулярного рассеяния и ослабления на аэрозолях. Для однородной атмосферы кривые можно использовать непосредственно. Если атмосфера неоднородна, необходимо сначала определить эквивалентную длину трассы по методике, приведенной в работе [10]. В этой работе содержится также много других кривых для отдельных компонентов атмосферы. Порядок определения коэффициента пропускания по кривым фиг. 2.15—2.19 следующий. Соответствующая шкала коэффициента пропускания наносится на прозрачную бумагу. Совмещая заданное количество поглотителя (или длину трассы) с горизонтальной линией и передвигая шкалу на заданную длину волны, считывают значение коэффициента пропускания для этой длины волны на пересечении шкалы с кривой.
2.15—2.19 следующий. Соответствующая шкала коэффициента пропускания наносится на прозрачную бумагу. Совмещая заданное количество поглотителя (или длину трассы) с горизонтальной линией и передвигая шкалу на заданную длину волны, считывают значение коэффициента пропускания для этой длины волны на пересечении шкалы с кривой.
Концентрация паров воды как поглотителя выражается различными способами. Основной мерой является абсолютная влажность — масса воды в граммах на 1 см3 объема воздуха, содержащего пары воды, при определенных температуре и давлении.
Фиг. 2.15. Молекулярное пропускание паров воды в дискретных линиях [10].
Фиг. 2.16. Молекулярное пропускание паров воды в непрерывном спектре, уширенном давлением [10].
Фиг. 2.17. Молекулярное пропускание равномерно распределенной смеси С02, N20, СО и СН4 [10].
Фиг. 2.18. Пропускание, обусловленное молекулярным рассеянием всех компонентов атмосферы [10].
Фиг. 2.19. Пропускание аэрозолей [10]. 1 — поглощение; 2 — рассеяние.
1 — поглощение; 2 — рассеяние.
Абсолютная влажность На (г/см3) является функцией парциального давления Р (мм рт. ст.) паров воды и температуры Та (К). Абсолютная влажность насыщенного парами воды воздуха равна
(2.21)
где парциальное давление Р также зависит от температуры Та. Более простой мерой концентрации поглотителя является относительная влажность, представляющая собой отношение абсолютной влажности в определенных условиях к абсолютной влажности, соответствующей насыщенному объему при тех же условиях.
Абсолютная и относительная влажности не определяют непосредственно количество поглотителя на длине данной трассы. Мерой, определяющей суммарное поглощение на трассе, является количество осажденной воды, которое можно найти по относительной влажности и длине трассы. Количество осажденной воды w характеризуется толщиной слоя жидкой воды, образовавшейся при конденсации паров в цилиндре, длина которого равна длине трассы. Эта толщина обычно выражается в сантиметрах осажденной воды на километр трассы (см/км).
Величина w связана с плотностью жидкой воды d, относительной влажностью Нт (выраженной в долях единицы) и абсолютной
Фиг. 2.20. Количество осажденной воды (см/км) и абсолютная влажность в условиях насыщения в зависимости от температуры.
влажностью На следующим образом:
Полное количество осажденной воды на трассе wT выражается в сантиметрах. Если абсолютная и относительная влажности на трассе постоянны, полное количество осажденной воды получается умножением величины w (см/км) на длину трассы R (км). На фиг. 2.20 показаны толщина слоя осажденной воды и абсолютная влажность в условиях насыщения в функции температуры.
Потери на поглощение, равные 0,1Ь7 при wT = 0, обусловлены ослаблением излучения другими компонентами атмосферы. Для окна 3—5 мкм не выявляется столь явной зависимости от wT. Это связано с тем, что в окне 3—5 мкм поглощение углекислым газом проявляется в большей степени, чем в окне 8—14 мкм.
Принципы, изложенные в работе [10], были положены в основу программы для ЭВМ, разработанной Селби и Макклэтчем [18]. Эта программа была использована Макдональдом [19] для получения кривых, представленных на фиг. 2.22—2.42. Для сравнения потерь при пропускании в диапазоне 3—5 и 8—12 мкм Макдональд выбрал три наклонных трассы протяженностью 30, 15 и 7,5 км и три высоты 90, 1220 и 3660 м. Использованы две модели атмосферы: тропические условия и стандартная атмосфера США 1962 г., обе с дымкой и без дымки. Изменения пропускания при различных метеорологических дальностях видимости на различных высотах и расстояниях для диапазона 8—12 мкм показаны на фиг. 2.22— 2.27, а для диапазона 3—5 мкм — на фиг. 2.28—2.33. Различия между тропическими условиями и стандартной атмосферой США для различных высот и протяженностей наклонных трасс в диапазоне 8—12 мкм показаны на фиг. 2.34—2.42.
Эта программа была использована Макдональдом [19] для получения кривых, представленных на фиг. 2.22—2.42. Для сравнения потерь при пропускании в диапазоне 3—5 и 8—12 мкм Макдональд выбрал три наклонных трассы протяженностью 30, 15 и 7,5 км и три высоты 90, 1220 и 3660 м. Использованы две модели атмосферы: тропические условия и стандартная атмосфера США 1962 г., обе с дымкой и без дымки. Изменения пропускания при различных метеорологических дальностях видимости на различных высотах и расстояниях для диапазона 8—12 мкм показаны на фиг. 2.22— 2.27, а для диапазона 3—5 мкм — на фиг. 2.28—2.33. Различия между тропическими условиями и стандартной атмосферой США для различных высот и протяженностей наклонных трасс в диапазоне 8—12 мкм показаны на фиг. 2.34—2.42.
Толщина слоя осажденной воды на трассе wJf см
Фиг. 2.21. Средний коэффициент пропускания в зависимости от полного количества осажденной воды для пяти спектральных диапазонов [15].
Результаты свидетельствуют, что без учета характеристик источников и приемников излучения для сухого воздуха в средних широтах пропускание в диапазоне 8—12 мкм больше, чем в диапазоне 3—5 мкм, поскольку в последнем диапазоне имеет место сильное поглощение углекислым газом. В чистой тропической атмосфере с высокой влажностью пропускание выше в диапазоне 3—5 мкм, так как пары воды сильно поглощают излучение в диапазоне 8— 12 мкм. Но дымка приводит к более сильному ослаблению излучения в диапазоне 3—5 мкм по сравнению с диапазоном 8—12 мкм, и именно это заставляет отдать предпочтение диапазону 8—12 мкм в связи с тем, что долгое отсутствие дымки во влажном тропическом воздухе маловероятно. Однако основной интерес представляет не абсолютная величина коэффициента пропускания, а соотношение тепловой чувствительности и коэффициента пропускания.
В чистой тропической атмосфере с высокой влажностью пропускание выше в диапазоне 3—5 мкм, так как пары воды сильно поглощают излучение в диапазоне 8— 12 мкм. Но дымка приводит к более сильному ослаблению излучения в диапазоне 3—5 мкм по сравнению с диапазоном 8—12 мкм, и именно это заставляет отдать предпочтение диапазону 8—12 мкм в связи с тем, что долгое отсутствие дымки во влажном тропическом воздухе маловероятно. Однако основной интерес представляет не абсолютная величина коэффициента пропускания, а соотношение тепловой чувствительности и коэффициента пропускания.
Фгтг. 2.22. Пропускание атмосферы.
Наклонная трасса 7,5 км; стандартная атмосфера США 1962 г.;— дымна
и аэрозоли отсутствуют; — — — дымка, метеорологическая дальность видимости 5 км. 1 — высота 3,66 км; 2 — высота 1,22 км; з — высота 90 м.
Фиг. 2.23. Пропускание атмосферы.
Длина волны, мим
Наклонная трасса 7,5 км; тропическая атмосфера; дымка
и аэрозоли отсутствуют; — — — дымка, метеорологическая дальность видимости 5 км.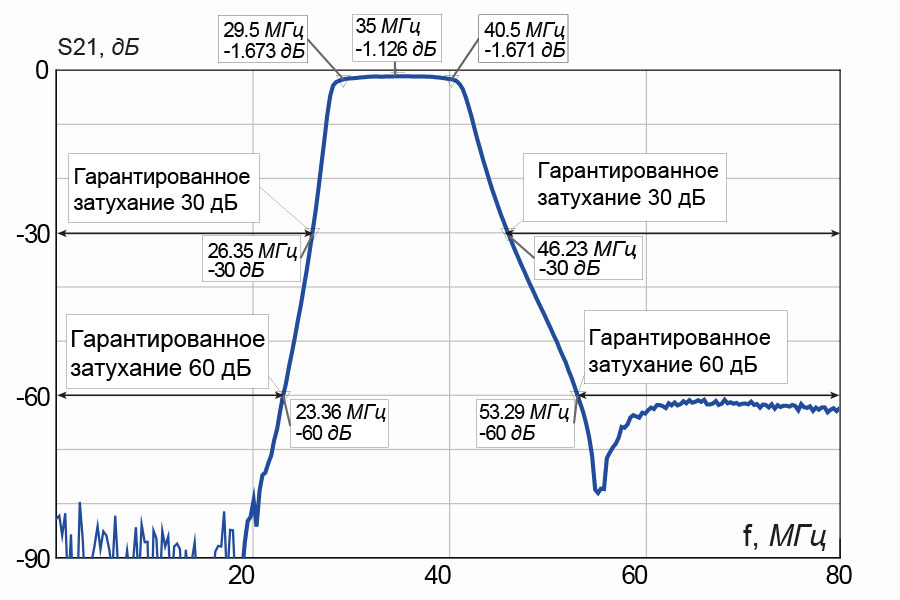 1 — высота 3,66 км; 2 — высота 1,22 км; 3 — высота 90 м.
1 — высота 3,66 км; 2 — высота 1,22 км; 3 — высота 90 м.
Фиг. 2.24. Пропускание атмосферы.
Наклонная трасса 15 км; стандартная атмосфера США 1962 г.;
дымка и аэрозоли отсутствуют; — — — дымка, метеорологическая дальность видимости 5 км. 1 — высота 3,66 км; 2 — высота 1,22 км; 3 — высота 90 м.
Фиг. 2.25. Пропускание атмосферы.
Наклонная трасса 13 км; тропическая атмосфера;— дымка
и аэрозоли отсутствуют;—- дымка, метеорологическая
дальность видимости 5 км. 1—высота 3,66 км; 2 — высота
- км; 3 — высота 90 м.
Фиг. 2.26. Пропускание атмосферы.
Наклонная ‘трасса 30 км; стандартная атмосфера США 1962 г.;———————
дымка и аэрозоли , отсутствуют; — — — дымка, метеорологическая дальность видимости 5 км. I — высота 3,66 км; 2 — высота 1»22 км.
Фиг. 2.27. Пропускание атмосферы.
Наклонная трасса 30 км; тропическая атмосфера;———— дымка и аэрозоли отсутствуют; дымка, метеорологическая дальность видимости 5 км.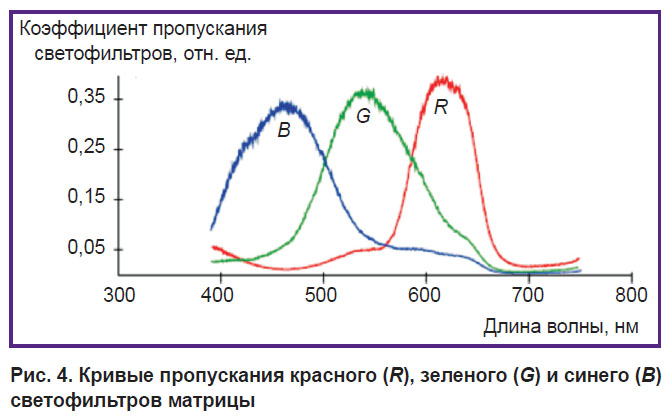 1 — высота 3,66; 2 — высота 1*22 км.
1 — высота 3,66; 2 — высота 1*22 км.
Фиг. 2.28. Пропускание атмосферы.
Наклонная трасса 7,5 км; стандартная атмосфера США 1962 г.,—————————— дымка и аэрозоли
отсутствуют; — —>— дымка, метеорологическая дальность видимости 5 км. 1 —высота 3,66 км; 2 — высота 1,22 км; з — высота 90 м.
Фиг. 2.29. Пропускание атмосферы.
Наклонная трасса 7,5 км; тропическая атмосфера; дымка и аэрозоли отсутствуют;
— — — дымка, метеорологическая дальность видимости 5 км. 1 — высота 3,66 км; 2 — высота 1,22 км; з’л— высота 90 м.
Фиг. 2.30. Пропускание атмосферы.
Наклонная трасса 15 км; стандартная атмосфера США 1962 г.; дымка аэрозоли
отсутствуют; — — — дымка, метеорологическая дальность видимости 5 км. 1 — высота 3,60 км; 2 — высота 1,22 км; 3 — высота 90 м.
Фиг. 2.31. Пропускание атмосферы.
Наклонная трасса 15 км; тропическая атмосфера;————— дымка и аэрозоли отсутствуют;
— — — дымка, метеорологическая дальность видимости 5 км.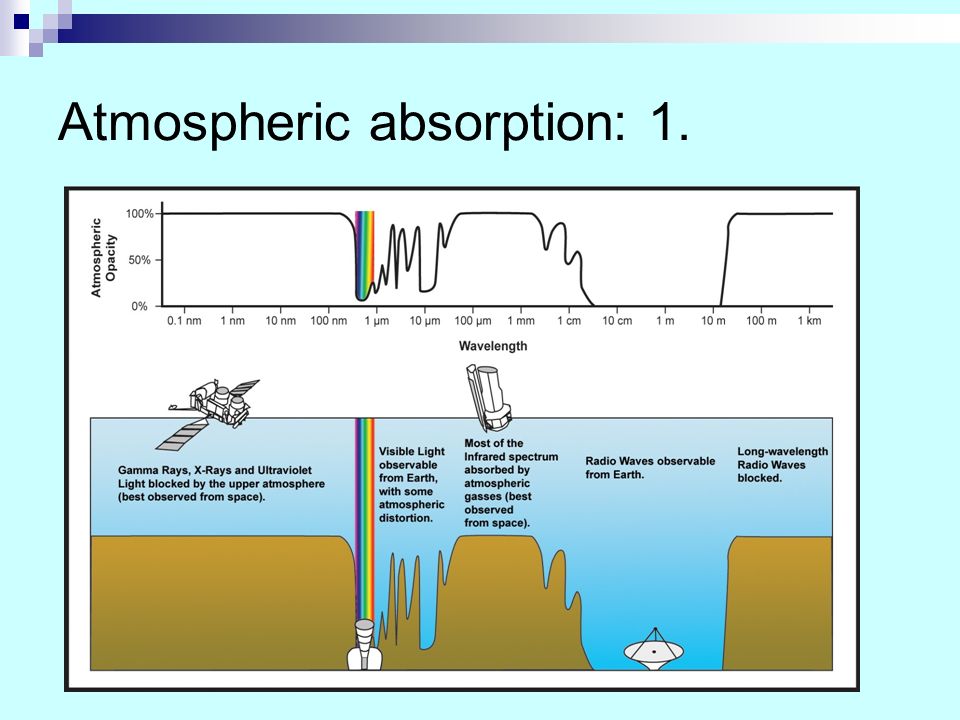 1 — высота 3,66 км; 2 — высота 1,22 км; 3 — высота 90 м.
1 — высота 3,66 км; 2 — высота 1,22 км; 3 — высота 90 м.
Фиг. 2.32. Пропускание атмосферы.
Наклонная трасса 30 км; стандартная атмосфера США 1962 г.;——— дымка и аэрозоли
отсутствуют; — — — дымка, метеорологическая дальность видимости 5 км. 1 — высота 3,66 км; 2—высота 1,22 км.
Фиг. 2.33. Пропускание атмосферы.
Наклонная трасса 30 км; тропическая атмосфера;————— дымка и аэрозоли отсутствуют;
————- дымка, метеорологическая дальность видимости 5 км. 1 — высота 3,66 км;
2 — высота 1,22 км.
Фиг. 2.34. Пропускание атмосферы.
Высота 150 м; наклонная трасса 1,5 км; ————————— стандартная атмосфера США 1962 г.;
————— тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; з — метеорологическая дальность видимости 5 км.
Фиг. 2.35. Пропускание атмосферы.
Высота 150 м; наклонная трасса 4,5 км;—- стандартная атмосфера США 1962 г.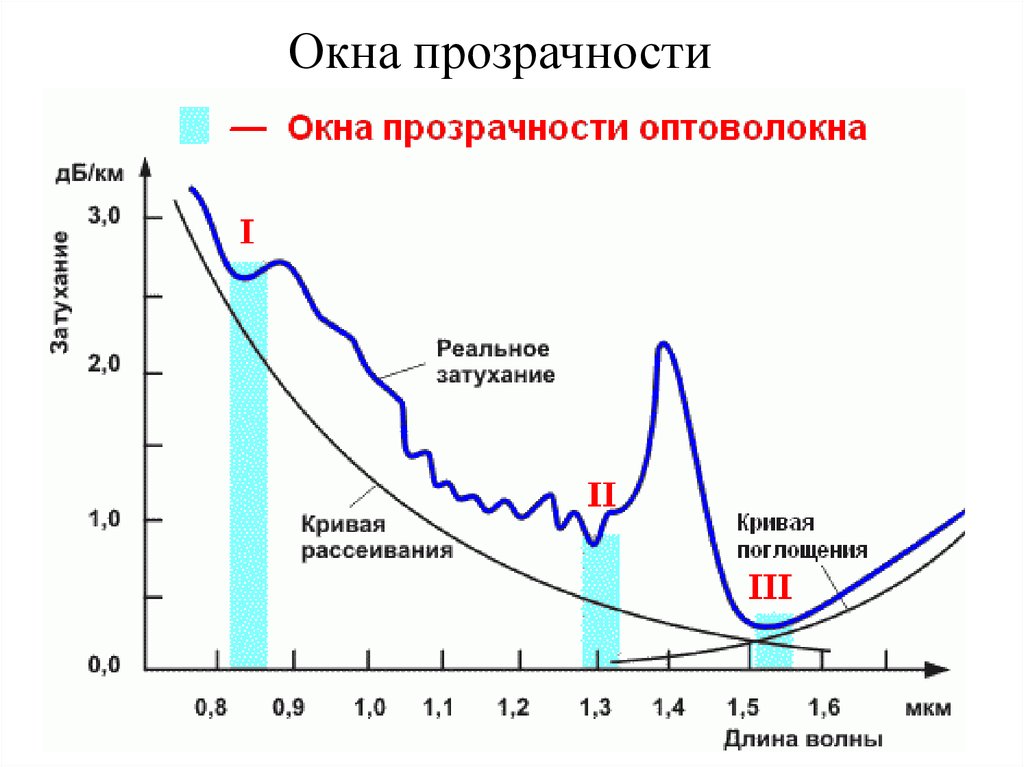 ;
;
- — — тропическая атмосфера. J — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; 3 — метеорологическая дальность видимости 5 км.
Фиг. 2.36. Пропускание атмосферы.
Высота 150 м; наклонная трасса 17,5 км; ————— стандартная атмосфера США 19G2 г.;
————- тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; 3 — метеорологическая дальность видимости 5 км.
Фиг. 2.37. Пропускание атмосферы.
Высота 600 м; наклонная трасса 1,5 км; ——- стандартная атмосфера США 1962 г.;
— — — тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; з — метеорологическая дальность видимости 5 км.
Фиг. 2.38. Пропускание атмосферы.
Высота 600 м; наклонная трасса4,5 км;——— стандартная атмосфера США 1962 г.;——————
тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; з — метеорологическая дальность видимости 5 км.
Фиг. 2.39. Пропускание атмосферы.
Высота 600 м; наклонная трасса 15 км; —————— стандартная атмосфера США 1962 г.;
——————- тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; 3 — метеорологическая дальность видимости 5 км.
Фиг. 2.40. Пропускание атмосферы.
Высота 3 км; наклонная трасса 4,5 км; ———————— стандартная атмосфера США 1962 г.;
- — — тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; з — метеорологическая дальность видимости 5 км.
Фиг. 2.41. Пропускание атмосферы.
Высота 3 км; наклонная трасса 15 км; —————— стандартная атмосфера США 1962 г.;
——— — тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; з — метеорологическая дальность видимости 5 км.
Фиг.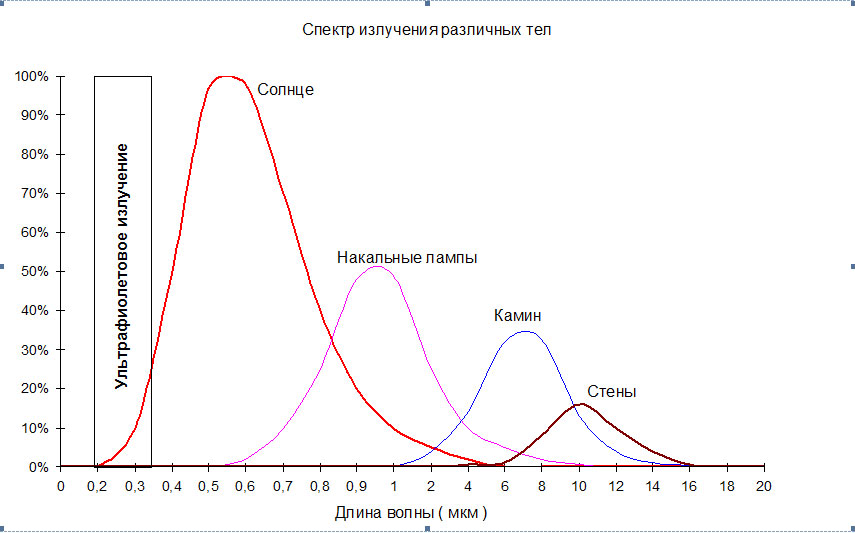 2.42. Пропускание атмосферы.
2.42. Пропускание атмосферы.
Высота 11 км; наклонная трасса 15 км; ——————— стандартная атмосфера США 1962 г.;
- — — тропическая атмосфера. 1 — дымка и аэрозоли отсутствуют; 2 — метеорологическая дальность видимости 23 км; 3 — метеорологическая дальность видимости 5 км.
С этой точки зрения диапазон 8—12 мкм предпочтительнее диапазона 3—5 мкм из-за существенной разницы в чувствительности Ь этих диапазонах даже при отсутствии потерь на пропускание (см. разд. 5.12).
Сравнение пропускания атмосферы в двух спектральных диапазонах на протяженных морских трассах сделано Егером и др. [20]. Используя в радиометре приемники излучения на основе InSb и (Hg, Cd)Te с высокими параметрами, авторы экспериментально подтвердили, что на трассах протяженностью 1—13 км в условиях ограничения шумами внешнего фона (изменяющаяся морская поверхность) диапазон 8—14 мкм имеет преимущества в пропускании сигнала.
ЛИТЕРАТУРА
- Брамсон М.
 А., Инфракрасное излучение нагретых тел, «Наука», 1964.
А., Инфракрасное излучение нагретых тел, «Наука», 1964. - Джемисон Дж. Э. и др., Физика и техника инфракрасного излучения, изд-во «Советское радио», М., 1965.
- Merritt Т. P., Hall F. F., Blackbody Radiation, Proc. IRE, 47, 1435— 1441 (1959).
- Jones R. C., Terminology in Photometry and Radiometry, JOS A, 53, 1314-1315 (1963).
- Хадсон P., Инфракрасные системы, изд-во «Мир», М., 1972.
- Hadni A., Essentials of Modern Physics Applied to the Study of the Infrared, Pergamon, N. Y., 1967.
- Wolfe W. L., Ed., Handbook of Military Infrared Technology, Superintendent of Documents, U. S. Government Printing Office, 1965.
- Круз П., Макглоулин JI., Макквистан Р., Основы инфракрасной техники, Воениздат, М., 1964.
- Seyrafi К., Ed., Engineering Design Handbook: Infrared Military Systems, Pt. 1, U. S. Army Materiel Command Pamphlet 706—127.
- McClatchey R. A.,FennR. W., Selby J. E. A., Volz F. E., Garing J. S., Optical Properties of the Atmosphere, U.
 S. Air Force Cambridge Research Laboratories report AFCRL-72-0497, Hanscom Field, Massachusetts, 1972.
S. Air Force Cambridge Research Laboratories report AFCRL-72-0497, Hanscom Field, Massachusetts, 1972. - Farrow J. B., Gibson A. F., Influence of the Atmosphere on Optical Systems, Optica Acta, 17, 317—336 (1970).
- Taylor J. H., Yates H. W., Atmospheric Transmission in the Infrared, JOS A, 47, 223—226 (1957).
- Streete J. L., Infrared Measurements of Atmospheric Transmission at Sea Level, Appl. Opt., 7, 1545-1549 (1968).
- Anding D., Band-Model Methods for Computing Atmospheric Slant-Path Molecular Absorption, IRIA State of the Art Report 7142-21-T, February 1967, reprinted 1969.
- Hodges J. A., Aerosol Extinction Contribution to Atmospheric Absorption in Infrared Wavelengths, Appl. Opt., 11, 2304-2310 (1972).
- Hodges J. A., Xerox Electro-Optical Systems, Pasadena, California (частное сообщение).
- Moser P. A., Naval Air Development Center, Warminster, Pennsylvania (частное сообщение).
- Selby J. E. A., McClatchey R. М., Atmospheric Transmittance from 0.
 25 to 28.5fxm: Computer code LOWTRAN 2, U.S.A.F. Cambridge Research Laboratories Report AFCRL-72-0745, 1972.
25 to 28.5fxm: Computer code LOWTRAN 2, U.S.A.F. Cambridge Research Laboratories Report AFCRL-72-0745, 1972. - MacDonald D. A., Honeywell Radiation Center, Lexington, Massachusetts (частное сообщение).
- Jaeger Т., Nordbryhn A., Stockseth P. A., Detection of Low Contrast Targets at 5цт and Юцт: A Comparison, Appl. Opt., 11, 1833-1835 (1972).
- Назад
- Вперёд
- Назад
- Вперёд
- Вы здесь:
- Главная
- Архив
- Разное архив
- Электрооборудование торфопредприятий
Еще по теме:
- Вспомогательные устройства при тепловизионном обследовании
- Классификация тепловизоров и получение ими изображения
- Краткая характеристика современных тепловизоров
- Тепловизоры для строительной диагностики
- Типовые модели тепловизоров
Пропускание — frwiki.
 wiki
wiki
Коэффициент пропускания, как правило, представляет собой коэффициент, характеризующий передачу переменной в системе. Он рассчитывается как соотношение между входной и выходной величиной. Обычно выражается в процентах (0% для непрозрачного материала).
Термин « прозрачность» скорее относится к англоязычной области. Тексты на французском языке часто предпочитают другие выражения в качестве фактора передачи .
Резюме
- 1 оптический
- 2 Биология
- 3 Электронный и автоматический
- 4 Коэффициент теплопередачи
- 5 ссылки
- 6 См. Также
Оптический
Пример: непрозрачность атмосферы в соответствии с длиной волны электромагнитных волн (включая видимый свет) между космосом и земной почвой. Более строго, эта диаграмма представлена в процентах; 100% будет считаться нулевым коэффициентом пропускания (бесконечная непрозрачность).1-Т{\ displaystyle 1 — {\ mathcal {T}}}
В оптике коэффициент пропускания или коэффициент пропускания оптической системы — это отношение интенсивности передаваемого излучения к интенсивности падающего излучения. Это определение по передаваемой интенсивности подразумевает зеркальный поток.
Это определение по передаваемой интенсивности подразумевает зеркальный поток.
Если отметить I 0 — интенсивность падающего света и I — передаваемую интенсивность, тогда коэффициент пропускания будет иметь значение:
- Тзнак равнояя0.{\ displaystyle T = {\ frac {I} {I_ {0}}}.}
В оптическом приборе коэффициент передачи может определяться соотношением между передаваемой яркостью и падающей яркостью.
Когда мы рассматриваем диффузное излучение, мы определяем коэффициент пропускания как долю передаваемого светового потока или падающего потока энергии . В области сенситометрии, в фотографии, это соотношение можно назвать прозрачностью, обратной непрозрачности . При необходимости мы можем отделить зеркальный поток от диффузного.
Коэффициент пропускания можно измерить по всей видимой области или около заданной длины волны . Распределение коэффициентов пропускания в зависимости от длины волны в однородной пластине без рассеяния, то есть в фильтре, является спектральным внутренним коэффициентом пропускания .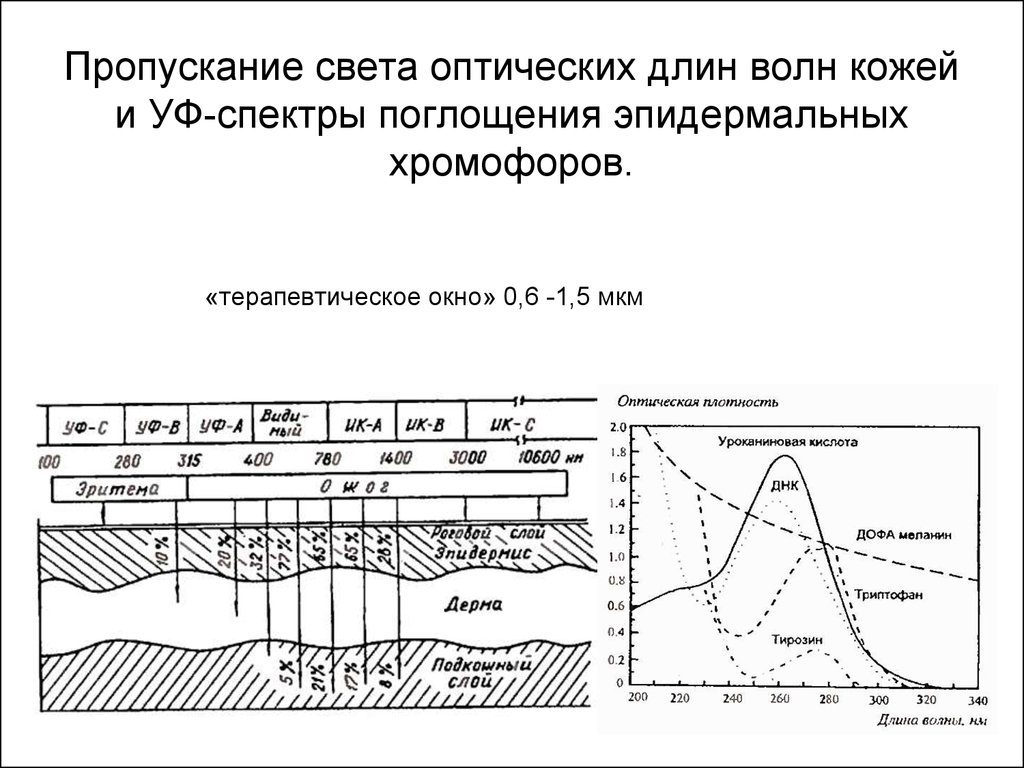 {- D}}, так сказать .Dзнак равно-бревноТ{\ Displaystyle D = — \ log T}
{- D}}, так сказать .Dзнак равно-бревноТ{\ Displaystyle D = — \ log T}
Биология
Коэффициент пропускания продукта через орган или другой биологический элемент — это соотношение между количеством, присутствующим в единицу времени на входе, и количеством, присутствующим на выходе. Например, можно рассчитать коэффициент пропускания креатинина почками.
Электронный и автоматический
В электронике коэффициент пропускания эквивалентен передаточной функции.
Когда мы рассматриваем логарифм доли передаваемой мощности, которая чаще всего выражается в децибелах, мы говорим об ослаблении и усилении . Волоконно-оптические телекоммуникации следуют тому же соглашению, и оптическая плотность на передачу является десятичным логарифмом обратной величины коэффициента передачи, как в сенситометрии.
Коэффициент теплопередачи
Теплоизоляции стен оценивает коэффициент теплопередачи или коэффициент теплопередачи коэффициент, который является «фактор нормы теплового потока ф по абсолютному значению разности температур Δ T » . Термин «коэффициент теплопередачи» в основном используется в строительной технике . В отличие от других коэффициентов пропускания, которые являются безразмерная, коэффициент теплопередачи имеет размерность MT -3 .Θ -2 и ее единица СИ является ватт на квадратный метр кельвин (Wm -2 .К -2 ).
Термин «коэффициент теплопередачи» в основном используется в строительной технике . В отличие от других коэффициентов пропускания, которые являются безразмерная, коэффициент теплопередачи имеет размерность MT -3 .Θ -2 и ее единица СИ является ватт на квадратный метр кельвин (Wm -2 .К -2 ).
Рекомендации
- ↑ a и b Международная электротехническая комиссия, Международный электротехнический словарь (IEC 60050) ,( 1- е изд. 1987 г.) ( прочитать строку ) : « Освещение. Эмиссионные, оптические свойства материалов. 845-04-59 «коэффициент пропускания » .
- ↑ Ричард Тайлле, Лоик Злодей и Паскаль Февр, Физический словарь, Брюссель, Де Бок ,, стр.
 694
694 - ↑ Жан Терриен и Франсуа Десвинь, La Photométrie, Париж, Presses Universitaires de France, колл. «Что я знаю? «( N O +1467), 1- е изд. , стр. 59
- ↑ Terrien and Desvignes 1972, стр. 58.
- ↑ Рене Буйо, Курс фотографии: техника и практика, Париж, Дюно ,, 206 с. ( ISBN 2-10-000325-9 ), стр.
 89
89 - ↑ IEC 60050 : « Освещение. Эмиссионные, оптические свойства материалов. 845-04-59 «коэффициент обычной передачи» » и « 845-04-63 «коэффициент диффузной передачи» » .
- ↑ IEC 60050 : « Освещение. Эмиссионные, оптические свойства материалов. 845-04-81 «Спектральный коэффициент внутреннего пропускания» »
- ↑ (in) ИЮПАК, Сборник химической терминологии : Рекомендации ИЮПАК ,, 2- е изд. , 450 с. ( ISBN 0-86542-684-8, читать онлайн ), стр.
 9
9 - ↑ Хосе-Филипп Перес, Оптика. Фонды и приложения, Париж, Дюно, сб. «Обучение физике»,, 7- е изд. ( ISBN 2-10-048497-4, уведомление BnF п о FRBNF39904000 ), р. 183
- ↑ IEC 60050 : « Освещение. Эмиссионные, оптические свойства материалов. 845-04-66 «Плотность оптическая при пропускании» » .
- ↑ IEC 60050 « Колебания, сигналы и связанные с ними устройства. Трансмиссионные характеристики и производительность; искажение. 702-07-28 «Изоморфное пропускание» » .

- ↑ IEC 60050 « Связь по оптоволокну. Характеристики распространения. 731-03-31 «коэффициент передачи» » .
- ↑ IEC 60050 « Связь по оптоволокну. Характеристики распространения. 731-03-32 «Плотность оптическая при пропускании» » .
- ↑ IEC 60050 : « Физика для электротехники. Термодинамика. 113-04-39 «Коэффициент теплопередачи, коэффициент теплопередачи» » .
Смотрите также
- Функция передачи
- Поглощение | Оптическая плотность | Непрозрачность
- Отражение
<img src=»https://fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Статья об атмосфере+пропускание от The Free Dictionary
Атмосфера+пропускание | Статья об атмосфере+прозрачность от The Free Dictionary
Атмосферный + коэффициент пропускания | Статья об атмосфере+пропускание в The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова отдельно:
атмосферный
коэффициент пропускания
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.
Полный браузер
?
- ▲
- Коэффициент пропускания атмосферы
- Атмосферный перенос и рассеивание
- Модель атмосферного транспорта
- Оценочное исследование модели атмосферного переноса
- Атмосферная мутность
- Атмосферная турбулентность
- Атмосферная турбулентность
- Атмосферная турбулентность
- Атмосферная турбулентность
- Отделение атмосферной турбулентности и диффузии
- Лаборатория атмосферной турбулентности и диффузии
- Сигнатуры, прогнозы и эксперименты атмосферных утилит
- Атмосферное ультрафиолетовое излучение Интегрированный код
- Прерыватель атмосферного вакуума
- Прерыватель атмосферного вакуума
- Прерыватель атмосферного вакуума в сборе
- Эксперимент по изучению атмосферной изменчивости
- Профиль атмосферной вертикальной температуры
- Атмосферная видимость
- Монитор атмосферной видимости
- Генератор атмосферной воды
- Генератор атмосферной воды
- Атмосферная волна
- Атмосферный волновод
- Атмосферное окно
- Атмосферное окно
- Атмосферное окно
- Атмосферные окна
- Атмосферные окна
- Атмосферный рентгеновский спектрометр
- Атмосферное+пропускание
- Атмосферное, биологическое и химическое моделирование
- Атмосферные, экологические и водные ресурсы
- Атмосферная, морская и прибрежная среда
- Физика атмосферы, океана и планет
- Департамент атмосферных, океанических и космических наук
- Химическая ионизация при атмосферном давлении
- отверждение при атмосферном давлении
- Плазма атмосферного давления
- отверждение паром при атмосферном давлении
- вакуумный прерыватель атмосферного типа
- атмосферный
- атмосферный
- атмосферный
- атмосферно
- атмосферно
- атмосферно
- Индекс атмосфероустойчивости растительности
- атмосферники
- атмосферники
- атмосферники
- атмосферники
- Атмосфера, магнитосфера и плазма в космосе
- атмосфера
- Атмосферология
- АТМОС
- АТМОТБ
- ПРИВОД
- АТМП
- АТМП
- АТМФ
- ▼
Сайт:
Следовать:
Делиться:
Открыть / Закрыть
Atmospheric Transmittances :: Интернет-книга Ocean Optics
[Говард Гордон также внес свой вклад в эту страницу. ]
]
Уравнения, такие как (3) на странице «Формулировка проблемы» и
(13) на странице «Нормализованные отражения» включают в себя различные прямые
(Т) и
диффузный (t)
условия передачи в атмосфере, которые требуют обсуждения.
Прямая передача
Прямая передача через атмосферу используется, если только один конкретный путь или узкий
пучок почти коллинеарных путей, соединяющих источник и наблюдателя. Это
случай зеркального отражения, как показано на левой панели рис.
1. Когда датчик просматривает морскую поверхность, только небольшой участок
Морская поверхность видна как зеркальное отражение или прямой отблеск Солнца. Другой
точки на поверхности моря будут видны как локальные пятна солнечного блеска
для других направлений обзора, но не по направлению обзора датчика, как
показано. В каждом случае отраженное излучение распространяется в очень узком диапазоне
направлений, определяемых положением Солнца и законом отражения
(𝜃r=𝜃s для
Поверхность уровня). Узкие солнечные лучи бликуют для других направлений обзора.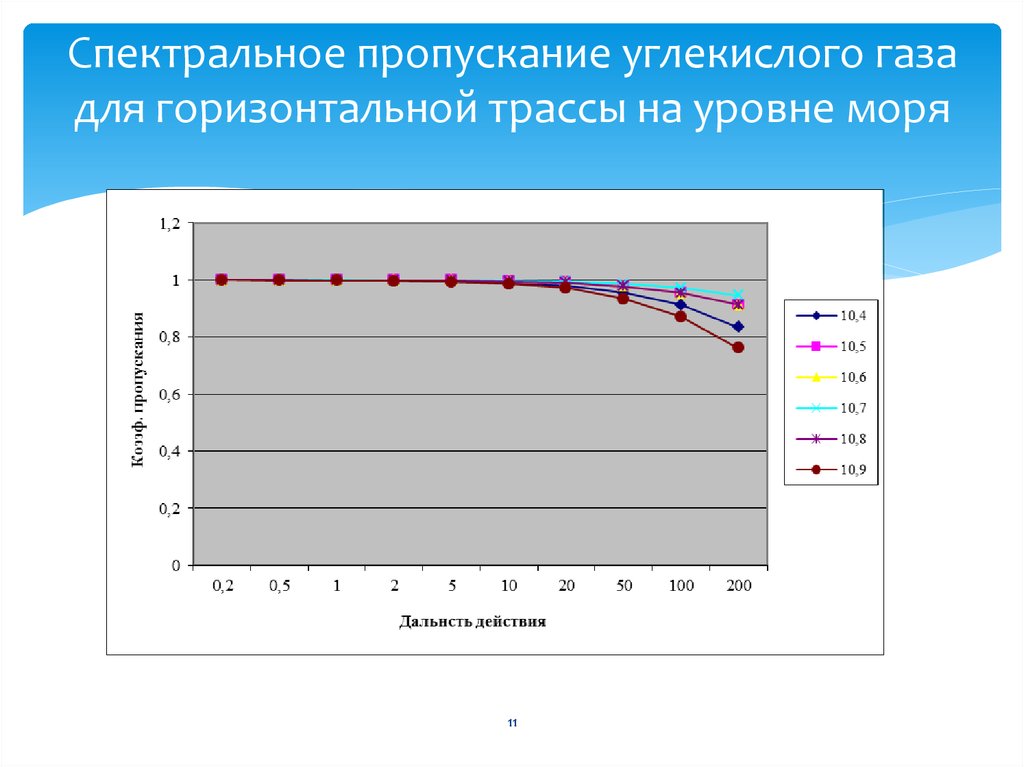
представлены пунктирной и штриховой линиями на левой панели рисунка. Эти
лучи могут влиять на интересующее направление только через два рассеяния: первое
отраженного луча, а второй — в интересующем направлении. Такой
путь двухрассеяния показан светлой пунктирной линией. Две россыпи делают
вклад невидимых лучей зеркального отражения в интересующее направление
очень маленький.
Пусть τ будет
оптическая толщина атмосферы вдоль вертикальной траектории (направление обзора надира для
датчик). Это т
включает все эффекты атмосферного поглощения и затухания
все составляющие атмосферы. Для направления обзора вне надира
𝜃в,
прямое пропускание тогда просто
T(𝜃v)= exp(−τ∕ cos𝜃v). | (1) |
Эта геометрия аналогична закону Ламберта-Бера для
Яркость распространения луча через однородную среду:
L(r)=L(0) exp(−cr), где
c — затухание луча
коэффициент и r
это пройденное расстояние. В данном случае
В данном случае
τ=кра, где
ра это
расстояние через атмосферу на вертикальной (видимой в надире) траектории и
r=ra∕ cos𝜃v есть
длина атмосферного пути вдоль направления обзора.
Диффузное пропускание
Для водоотталкивающего сияния Lw,
каждая точка морской поверхности излучает восходящее сияние
Lw(𝜃,ϕ), как
показано на правой панели рис. 1. Излучение из всех мест и различных
направления могут быть рассеяны в интересующем направлении за счет только одного рассеяния, так как
показано пунктирной линией на правой панели рис. 1. Рассеянное излучение
луча вдоль направления обзора, таким образом, можно заменить с помощью одного
рассеяние от излучения, испускаемого соседней точкой, распространяющейся в
иное направление. Таким образом, диффузное пропускание зависит не только от
атмосферные свойства и направление взгляда, но и на угловое распределение
лв,
что вообще неизвестно. Эта ситуация аналогична диффузному затуханию
Кд из
нисходящая радиация в толще воды плоскопараллельного океана,
освещается во всех точках поверхности.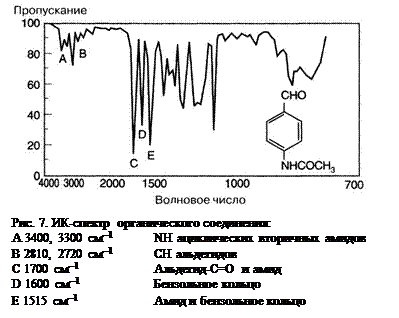 Потому что сияние поглощается или рассеивается
Потому что сияние поглощается или рассеивается
вне пути между источником и датчиком может быть заменено излучением
от других точек и направлений морской поверхности коэффициент диффузного пропускания
т(𝜃v)
будет больше прямого пропускания
T(𝜃v) (как и
диффузный коэффициент пропускания exp(−Kdz)
всегда больше, чем коэффициент пропускания луча
ехр(−cz)). Бухгалтерский учет
угловое распределение Lw
а для процессов рассеяния делает расчет коэффициента диффузного пропускания
сложнее, чем при прямой передаче.
Рис. 1. Левая панель: изображение солнечного блика, как видно из TOA, которое
описывается прямым пропусканием. Правая панель: Иллюстрация ухода воды.
сияние, как видно из TOA, которое описывается диффузным коэффициентом пропускания.
Рассеянный коэффициент пропускания выходящего из воды сияния вдоль конкретного просмотра
направление (𝜃v,ϕv)
по определению
| t(𝜃v,ϕv,λ)≡LwTOA(𝜃v,ϕv,λ)Lw(𝜃v,ϕv,λ), | (2) |
где Lw
— сияние, оставляющее воду на поверхности моря и
LwTOA
это уходящее из воды сияние, достигающее ТОА. Отныне все
Отныне все
предполагается, что величины являются функциями длины волны, а аргумент
λ будет опущен.
Один из способов вычисления t(𝜃v,ϕv)
состоит в том, чтобы запустить совмещенную модель переноса излучения океан-атмосфера для вычисления необходимого
Lw(𝜃v,ϕv) и
LwTOA(𝜃v,ϕv) для широкого
диапазон атмосферных и океанических условий, геометрия Солнца и обзора, а также длины волн.
Значения t(𝜃v,ϕv)
тогда будет получено с помощью уравнения. (2) и сведены в таблицу для последующего использования. Такие таблицы
должны быть построены для всех возможных типов аэрозолей (т. е. фазовая функция аэрозоля
формы), оптическая толщина аэрозоля, ВГД воды (или, по крайней мере, для хлорофилла
концентрации в водах Варианта 1) и геометрии просмотра. Столы бы
обязательно быть большим из-за большого количества параметров, которые могут повлиять на
t(𝜃v,ϕv).
Ян и Гордон (1997) исследовали вычисление диффузного
коэффициент пропускания и погрешности в нем на восстановленную яркость уходящей воды.
Используя комбинацию численного моделирования переноса излучения
океан и атмосфера и принципы взаимности, они сравнили
коэффициенты рассеянного пропускания, рассчитанные с использованием реалистичных смоделированных и измеренных
Лу(𝜃′,ϕ′)
распределения по сравнению с коэффициентами диффузного пропускания, рассчитанными в предположении, что
Лу изотропен.
Здесь Lu(𝜃′,ϕ′) обозначает
распределение восходящего подводного излучения прямо под поверхностью моря. Для уровня
поверхность моря, Lw(𝜃v,ϕv)=TF(𝜃′)Lu(𝜃′,ϕ′)∕nw2,
где сз
показатель преломления воды, в воде
𝜃′ относится к
𝜃v в эфире
Закон Снела sin𝜃v=nw sin𝜃′,
и ТФ(𝜃′)
— френелевский коэффициент пропускания поверхности из воды в воздух. Когда
Лу изотропен,
коэффициент диффузного пропускания не зависит от азимутального угла и обозначается
t∗(𝜃v).
Ян и Гордон (1997) (уравнение 3) показывают с умным использованием
взаимности, что рассеянное пропускание сияния
t∗ вдоль
атмосферный путь в направлении Солнца под зенитным углом Солнца
𝜃о есть
численно равен диффузному коэффициенту пропускания излучения от ТОА к
глубина непосредственно под поверхностью моря, при условии отсутствия апвеллинга
сияние в воде. То есть
| t∗(𝜃o)=ER(𝜃o)Fo cos(𝜃o)TF(𝜃o), | (3) |
, где ER(𝜃o) —
нисходящая плоская освещенность прямо под поверхностью моря для внеземного солнечного излучения
Фо инцидент на
TOA под углом 𝜃o,
и TF(𝜃o)
— пропускание Френелем поверхности моря вниз для излучения, падающего под углом
𝜃от нормального. С
С
восходящая яркость Lu(𝜃′,ϕ′)
используемого для получения этого результата, предполагается изотропным, азимутальная зависимость
t∗ есть
не имеет отношения к делу, и желаемое диффузное затухание для яркости в направлении взгляда
𝜃v=𝜃о есть
равным значению пропускания солнечной радиации при том же полярном угле.
великое достоинство уравнения (3) заключается в том, что он позволяет эффективно численно вычислять
t∗ с использованием
обратное (обратное) моделирование методом Монте-Карло нисходящей радиации для заданного
тип аэрозоля и оптическая толщина.
Полученное сияние, выходящее из воды, по уравнению. (2),
| Lw(𝜃v,ϕv)=LwTOA(𝜃v,ϕv)t(𝜃v,ϕv). | (4) |
Пусть Lw∗ обозначает
поиск при t∗
а не т
используется в уравнении (4). Ошибка в восстановленном сиянии воды, уходящей из-за использования
t∗, а не
точное т
ΔLwLw=Lw∗−LwLw=t−t∗t∗. | (5) |
Ян и Гордон (1997) обнаружили, что для углов обзора
ϕv
перпендикулярно главной плоскости (плоскости Солнца), ошибки в извлеченных
Lw не более 4%
для углов обзора 𝜃v≤45 град,
Зенитные углы солнца 𝜃o≤60 град,
и оптическая толщина аэрозоля, типичная для чистой атмосферы.
Ошибки в алгоритмах отношения полос были меньше; например, ошибка в
Lw(443)∕Lw(555) (используется
для получения концентрации хлорофилла) составляет менее 2%, за исключением очень чистой воды
и некоторые направления обзора, для которых погрешность соотношения составляет около 3%. Эти
диапазоны параметров покрывали большую часть потребностей SeaWiFS и ошибок этого
величины были сочтены приемлемыми по сравнению с другими ошибками в поиске
процесс (т. е. удаление излучения атмосферного пути). В этом случае
диффузное затухание можно получить с помощью предварительно вычисленных функций вида
| t∗(𝜃v)=A(𝜃v) exp[−B(𝜃v)τa]. | (6) |
где A(𝜃v) и
B(𝜃v) приведены в таблице для каждого
аэрозольного типа. Таким образом, для Н
Таким образом, для Н
углы 𝜃v,
только 2Н
числа А(𝜃v)
и B(𝜃v)
должны быть занесены в таблицу для каждого типа аэрозоля. Кроме того, тип аэрозоля и оптический
толщина определяется как часть процесса удаления аэрозоля
вклад в общую яркость пути. Это позволяет выбрать подходящие
Группа
τа и
оценка уравнения (4) оперативно выполнимо. Если аэрозоли игнорируются, уравнение. (6) уменьшает
к t∗(𝜃v)= exp[−12τR∕ cos𝜃v)],
где τR
оптическая толщина Рэлея. Это формула, использовавшаяся в первые дни для CZCS.
Атмосферная коррекция. Значение уравнения (6) заключается в том, что он допускает оптическую толщину аэрозоля
τа быть
включены в расчеты коэффициента диффузного пропускания с помощью простой экспоненциальной и
предварительно вычисленный А
и Б
ценности.
Однако для больших углов обзора вне надира
𝜃v, для азимутального просмотра
направления вблизи ϕv=0
или 180 град, а для очень чистой воды ошибки
ΔLw/Lw может быть как
целых 6%. Это может быть важно для датчика MODIS Aqua, который видит широкий
Это может быть важно для датчика MODIS Aqua, который видит широкий
диапазон ϕv
направления. Поэтому Гордон и Франц (2008) пересмотрели модель.
Янга и Гордона (1997) и разработали поправочный термин для
t∗ так
это уравнение (4) становится
| Lw(𝜃v,ϕv)=LwTOA(𝜃v,ϕv)t∗(𝜃v)[1+δ(𝜃v,ϕv)]. | (7) |
δ(𝜃v,ϕv)
фактор корректирует двунаправленные эффекты, возникающие в результате использования изотропного
Лу в расчете
t∗, а не точное,
неизотропный Lu(𝜃′,ϕ′).
Lu(𝜃′,ϕ′), необходимый для вычисления
δ был получен из
Lu=(f∕Q)(bb∕a) и на основе хлорофилла
модели для f∕Q
и bb∕a.
Опять же, δ
поправочный срок может быть предварительно рассчитан и сведен в таблицу для различных
типы аэрозолей и водные ВГД. Оценка воздействия
дельта
коррекция, примененная как к данным SeaWiFS, так и к данным MODIS Aqua, показала, что
полученные значения сияния, оставляющего воду, будут ошибочны не более чем
~1%, если
𝜃v<60 град и
поправка δ
опущено. Для 𝜃v>60 град,
то есть вблизи краев строк сканирования, использование
дельта
коррекция гарантирована.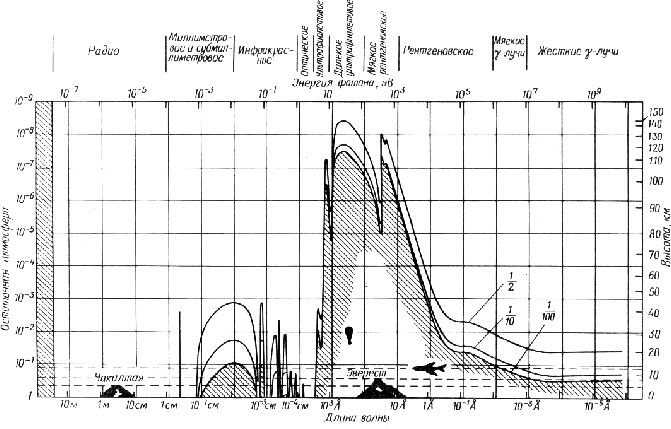
 А., Инфракрасное излучение нагретых тел, «Наука», 1964.
А., Инфракрасное излучение нагретых тел, «Наука», 1964. S. Air Force Cambridge Research Laboratories report AFCRL-72-0497, Hanscom Field, Massachusetts, 1972.
S. Air Force Cambridge Research Laboratories report AFCRL-72-0497, Hanscom Field, Massachusetts, 1972. 25 to 28.5fxm: Computer code LOWTRAN 2, U.S.A.F. Cambridge Research Laboratories Report AFCRL-72-0745, 1972.
25 to 28.5fxm: Computer code LOWTRAN 2, U.S.A.F. Cambridge Research Laboratories Report AFCRL-72-0745, 1972. 694
694 89
89 9
9
