Обозначение: высота, ширина, длина. Ширина

Построение чертежей — дело непростое, но без него в современном мире никак. Ведь чтобы изготовить даже самый обычный предмет (крошечный болт или гайку, полку для книг, дизайн нового платья и подобное), изначально нужно провести соответствующие вычисления и нарисовать чертеж будущего изделия. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.

Чтобы не возникло путаницы в понимании изображенного предмета и его параметров, во всем мире приняты условные обозначения длины, ширины, высоты и других величин, применяемых при проектировании. Каковы они? Давайте узнаем.

Величины

Площадь, длина, ширина, высота и другие обозначения подобного характера являются не только физическими, но и математическими величинами.

Единое их буквенное обозначение (используемое всеми странами) было уставлено в середине ХХ века Международной системой единиц (СИ) и применяется по сей день. Именно по этой причине все подобные параметры обозначаются латинскими, а не кириллическими буквами или арабской вязью. Чтобы не создавать отдельных трудностей, при разработке стандартов конструкторской документации в большинстве современных стран решено было использовать практически те же условные обозначения, что применяются в физике или геометрии.

Любой выпускник школы помнит, что в зависимости от того, двухмерная или трехмерная фигура (изделие) изображена на чертеже, она обладает набором основных параметров. Если присутствуют два измерения — это ширина и длина, если их три – добавляется еще и высота.

Итак, для начала давайте выясним, как правильно длину, ширину, высоту обозначать на чертежах.

Ширина

Как было сказано выше, в математике рассматриваемая величина является одним из трех пространственных измерений любого объекта, при условии что его замеры производятся в поперечном направлении. Так чем знаменита ширина? Обозначение буквой «В» она имеет. Об этом известно во всём мире. Причем, согласно ГОСТу, допустимо применение как заглавной, так и строчной латинских литер. Часто возникает вопрос о том, почему именно такая буква выбрана.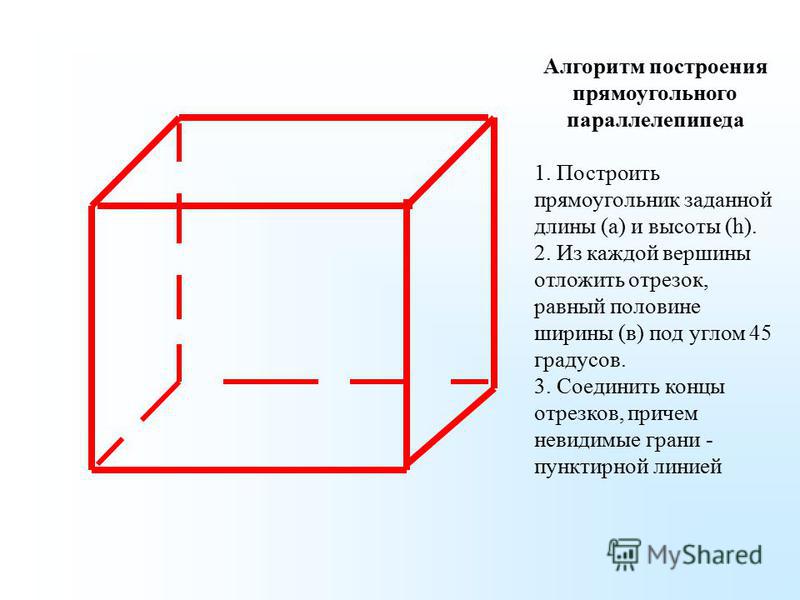 Ведь обычно сокращение производится по первой букве латинского, греческого или английского названия величины. При этом ширина на английском будет выглядеть как «width».

Вероятно, здесь дело в том, что данный параметр наиболее широкое применение изначально имел в геометрии. В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).

Большинство полагает, что это было сделано, дабы не путать ширину (обозначение буквой «B»/«b») с весом. Дело в том, что последний иногда именуется как «W» (сокращение от английского названия weight), хотя допустимо использование и других литер («G» и «Р»). Согласно международным нормам системы СИ, измеряется ширина в метрах или кратных (дольных) их единицах. Стоит отметить, что в геометрии иногда также допустимо использовать «w» для обозначения ширины, однако в физике и остальных точных науках такое обозначение, как правило, не применяется.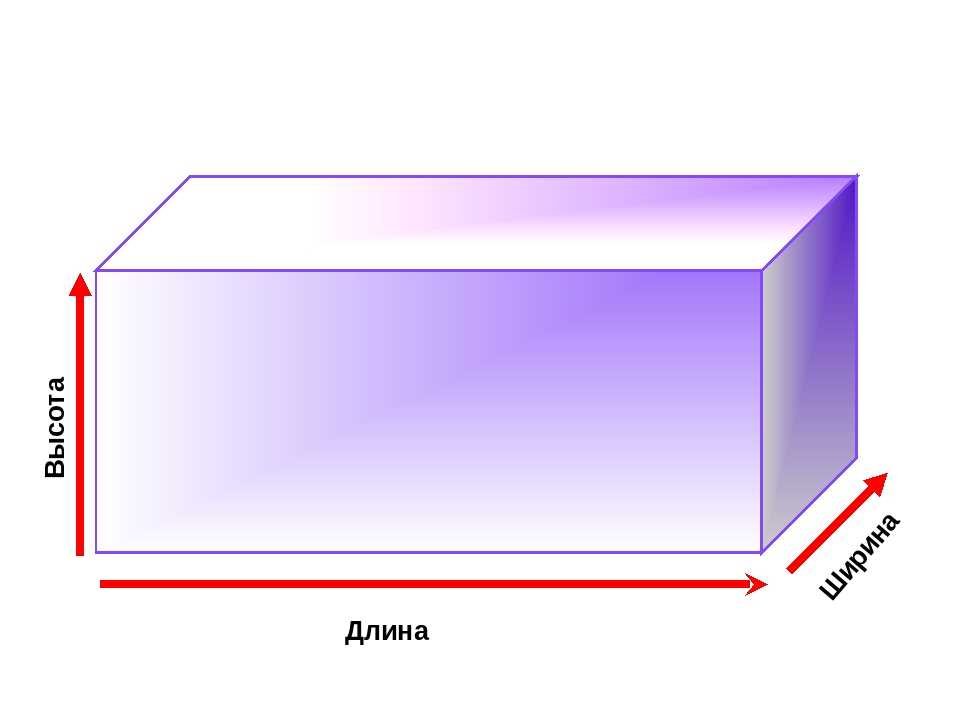

Длина

Как уже было указано, в математике длина, высота, ширина – это три пространственных измерения. При этом, если ширина является линейным размером в поперечном направлении, то длина — в продольном. Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.

В английском языке этот термин именуется length. Именно из-за этого данная величина обозначается заглавной или строчной начальной литерой этого слова — «L». Как и ширина, длина измеряется в метрах или их кратных (дольных) единицах.

Высота

Наличие этой величины указывает на то, что приходится иметь дело с более сложным — трехмерным пространством. В отличие от длины и ширины, высота численно характеризует размер объекта в вертикальном направлении.

На английском она пишется как «height». Поэтому, согласно международным нормам, ее обозначают латинской литерой «Н»/«h». Помимо высоты, в чертежах иногда эта буква выступает и как глубины обозначение. Высота, ширина и длина – все все эти параметры измеряются в метрах и их кратных и дольных единицах (километры, сантиметры, миллиметры и т. п.).

Радиус и диаметр

Помимо рассмотренных параметров, при составлении чертежей приходится иметь дело и с иными.

Например, при работе с окружностями возникает необходимость в определении их радиуса. Так именуется отрезок, который соединяет две точки. Первая из них является центром. Вторая находится непосредственно на самой окружности. На латыни это слово выглядит как «radius». Отсюда и общепринятое сокращение: строчная или заглавная «R»/«r».

Чертя окружности, помимо радиуса часто приходится сталкиваться с близким к нему явлением – диаметром. Он также является отрезком, соединяющим две точки на окружности. При этом он обязательно проходит через центр.

Численно диаметр равен двум радиусам. По-английски это слово пишется так: «diameter». Отсюда и сокращение – большая или маленькая латинская буква «D»/«d». Часто диаметр на чертежах обозначают при помощи перечеркнутого круга – «Ø».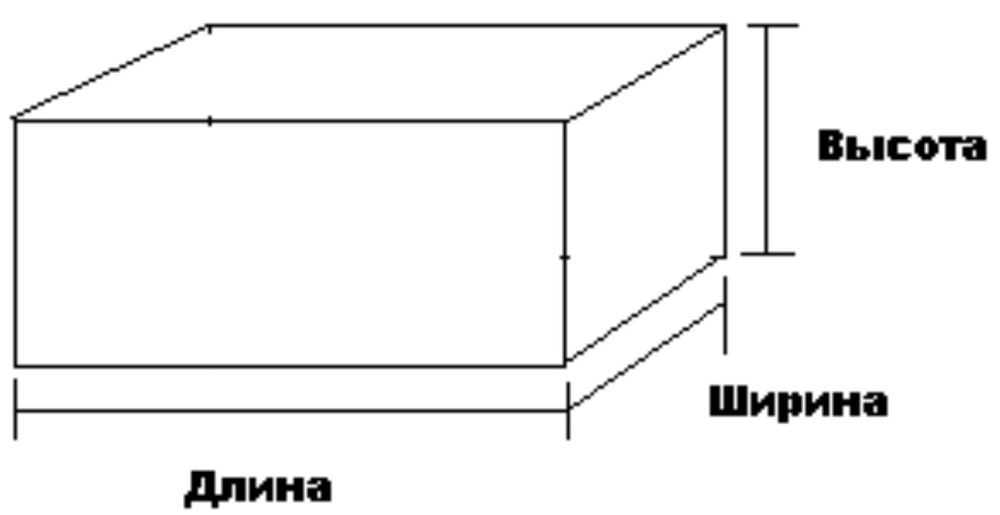

Хотя это распространенное сокращение, стоит иметь в виду, что ГОСТ предусматривает использование только латинской «D»/«d».

Толщина

Большинство из нас помнят школьные уроки математики. Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.

Почему так? Известно, что в случае с высотой, шириной, длиной, обозначение буквами можно было объяснить их написанием или традицией. Вот только толщина по-английски выглядит как «thickness», а в латинском варианте — «crassities». Также непонятно, почему, в отличие от других величин, толщину можно обозначать только строчной литерой. Обозначение «s» также применяется при описании толщины страниц, стенок, ребер и так далее.

Периметр и площадь

В отличие от всех перечисленных выше величин, слово «периметр» пришло не из латыни или английского, а из греческого языка.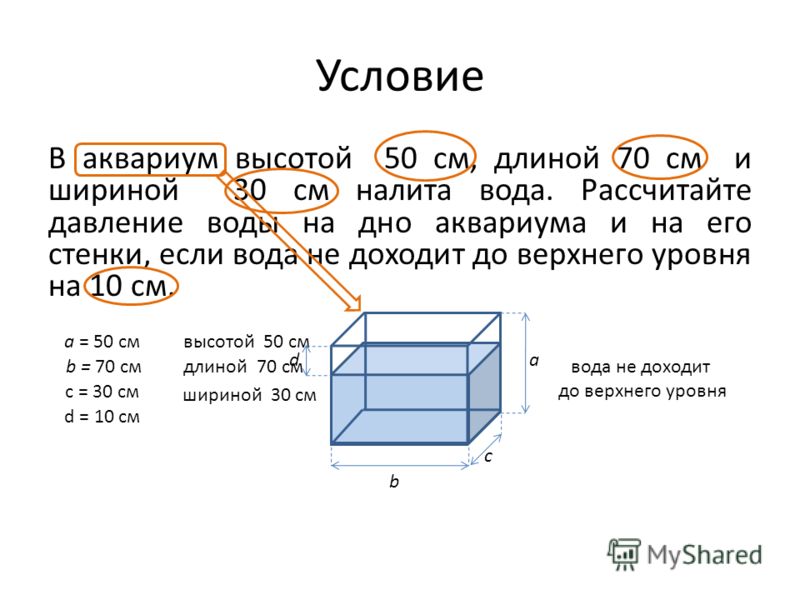 Оно образовано от «περιμετρέο» («измерять окружность»). И сегодня этот термин сохранил свое значение (общая длина границ фигуры). Впоследствии слово попало в английский язык («perimeter») и закрепилось в системе СИ в виде сокращения буквой «Р».

Площадь — это величина, показывающая количественную характеристику геометрической фигуры, обладающей двумя измерениями (длиной и шириной). В отличие от всего перечисленного ранее, она измеряется в квадратных метрах (а также в дольных и кратных их единицах). Что касается буквенного обозначения площади, то в разных сферах оно отличается. Например, в математике это знакомая всем с детства латинская литера «S». Почему так – нет информации.

Некоторые по незнанию думают, что это связано с английским написанием слова «square». Однако в нем математическая площадь – это «area», а «square» — это площадь в архитектурном понимании. Кстати, стоит вспомнить, что «square» — название геометрической фигуры «квадрат». Так что стоит быть внимательным при изучении чертежей на английском языке. Из-за перевода «area» в отдельных дисциплинах в качестве обозначения применяется литера «А». В редких случаях также используется «F», однако в физике данная буква означает величину под названием «сила» («fortis»).

Другие распространенные сокращения

Обозначения высоты, ширины, длины, толщины, радиуса, диаметра являются наиболее употребляемыми при составлении чертежей. Однако есть и другие величины, которые тоже часто присутствуют в них. Например, строчное «t». В физике это означает «температуру», однако согласно ГОСТу Единой системы конструкторской документации, данная литера — это шаг (винтовых пружин, заклепочных соединений и подобного). При этом она не используется, когда речь идет о зубчатых зацеплениях и резьбе.

Заглавная и строчная буква «A»/«a» (согласно все тем же нормам) в чертежах применяется, чтобы обозначать не площадь, а межцентровое и межосевое расстояние. Помимо различных величин, в чертежах часто приходится обозначать углы разного размера. Для этого принято использовать строчные литеры греческого алфавита.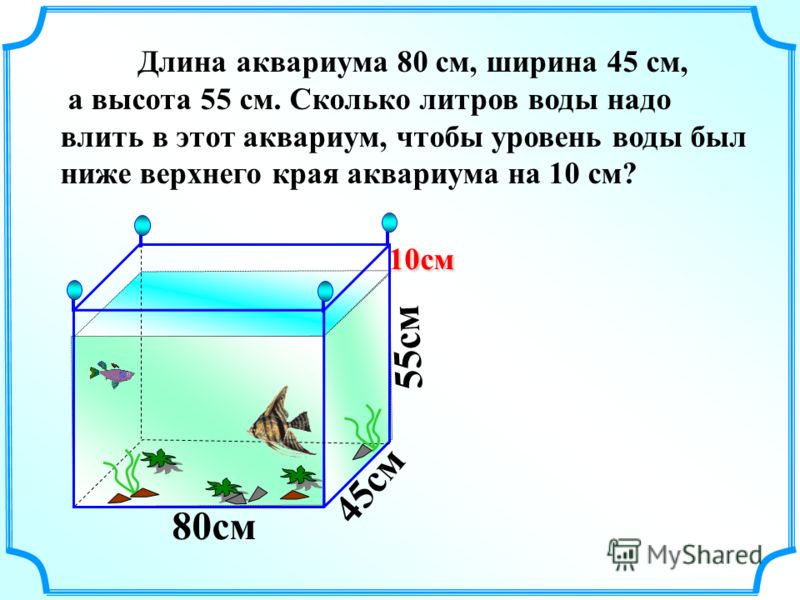 Наиболее применяемые — «α», «β», «γ» и «δ». Однако допустимо использовать и другие.

Какой стандарт определяет буквенное обозначение длины, ширины, высоты, площади и других величин?

Как уже было сказано выше, чтобы не было недопонимания при прочтении чертежа, представителями разных народов приняты общие стандарты буквенного обозначения. Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.

Для Российской Федерации таким нормативным документом является ГОСТ 2.321-84. Он был внедрен еще в марте 1984 г. (во времена СССР), взамен устаревшего ГОСТа 3452—59.

Высота ширина длина — латинские обозначения: как правильно пишутся размеры и чем отличаются величины

Решая геометрические задачи, ученики сталкиваются с вопросом: как правильно обозначить те или иные части чертежа? Например, высоту треугольника, ширину прямоугольника, размеры бассейна. Подобные обозначения мы найдем и в физических задачах: длина маятника, высота, с которой тело начинает падать… Поэтому следует знать некоторые правила.

Как обозначаются различные параметры

В единой системе измерения используется обозначение латинскими буквами:

• длину — буквой l, если речь идет об одной прямой линии: маятнике, рычаге, отрезке, прямой. Но если речь идет о геометрической фигуре, например, прямоугольнике, то используется А;
• высоту или глубину – h;
• ширину – В.

Что такое система СИ, ученики узнают лишь в средней школе, поэтому обычно в младших классах специального обозначениям для этих величин не вводят.

Как обозначить глубину?

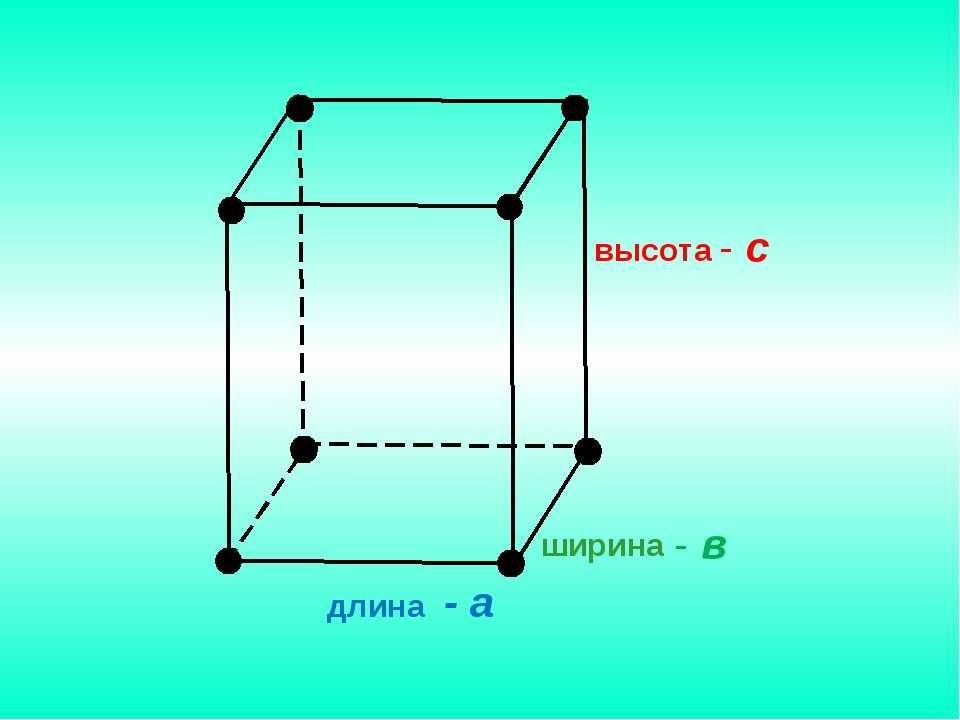
Почему же для высоты и глубины применяется одна и та же буква? Если вы построите чертеж параллелепипеда, то здесь вы отметите высоту фигуры.

А если составить чертеж прямоугольного бассейна того же размера, что и параллелепипед, то обозначается глубина. Таким образом, можно сказать, высота и глубина в этом случае будут одной величиной.

[warning]Внимание! Высота и глубина – две величины, которые обозначают один и тот же перпендикуляр, соединяющий две противоположные плоскости.[/warning]

Понятие «глубина» встречается и в географии. На картах она отображается цветом. Если речь идет о водных просторах, то чем темнее синий, цвет, тем больше глубина, а если речь идет о суше, то низменности обозначаются темно-зеленым цветом.

В черчении эта величина обозначается литерой S. Она позволяет создать полное восприятие объекта иногда даже с одним видом.

Что бывает длинным

Что же такое длина и как обозначается этот показатель? Она указывает расстояние от точки до точки, то есть размер отрезка. В геометрических задачах его принято обозначать как А. В стереометрии ее могут обозначать и А, и l (например, в задачах, где встречается прямая, пересекающая плоскость).

В физике же длина маятника, плеча рычага и т.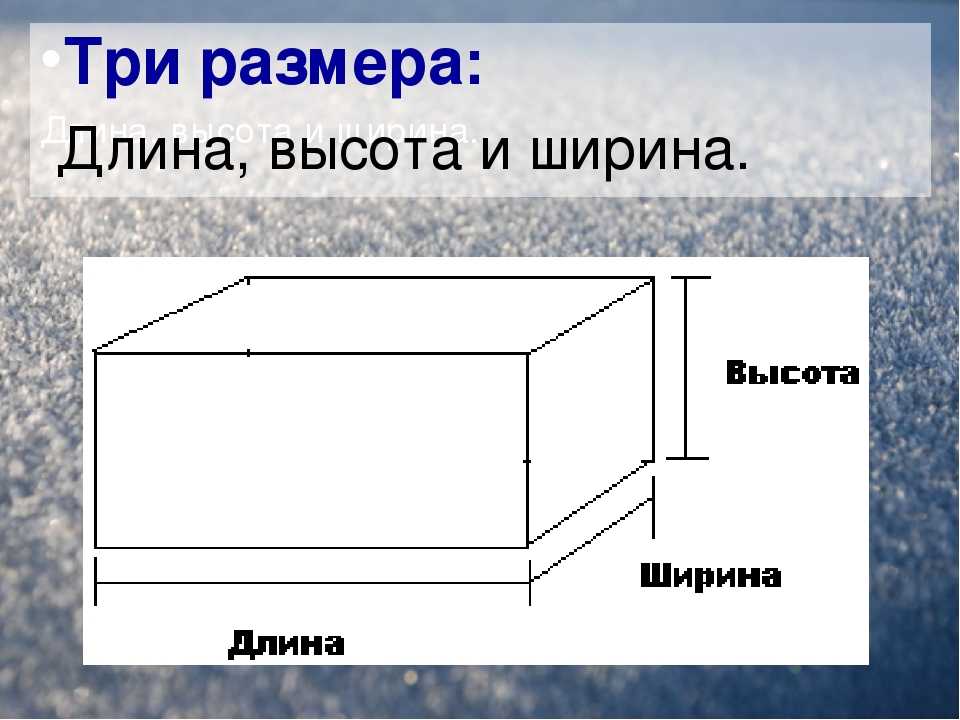 д. в «Дано» обозначается буквой l, так как речь идет об отдельной прямой.

Отличие длины от высоты

Длина – это величина, которая характеризует протяженность линии.

А высота – это перпендикуляр, опущенный на противолежащую плоскость.

То есть можно сделать вывод, что длина от высоты отличается тем, что является частью фигуры, совпадая с ее гранью, а высота получается в результате дополнительного построения на чертеже.

Высоту проводят для того, чтобы получить новые данные для решения задач, а также новых фигур в составе исходной.

Вот такой ширины

Ширина предмета необходима для того, чтобы понять форму как двумерного, так и трехмерного объекта. Как правило, она обозначается буквой В.

Измеряется ширина в метрах (по СИ). Но если предмет слишком мал, то для удобства используют более мелкие единицы измерения:

• дециметры,
• сантиметры,
• миллиметры,
• микрометры и т. д.

А если предмет слишком крупный, то пишутся такие приставки:

• Кило- (10³),
• Мега- (10⁶),
• Гига- (10⁹),
• Тера- (10¹²) и т.д.

Разумеется, такие крупные единицы измерения необходимы, например, для астрономии. Также они применяются в квантовой физике, микробиологии и так далее.

Как называются стороны прямоугольника?

В отличие от квадрата, стороны прямоугольника попарно равны и параллельны.

Это значит, что стороны, образующие углы различны.

Как правило, более длинную сторону прямоугольника называют длиной, а ширина прямоугольника — это его короткая сторона.

[stop]Важно! Зная такие данные, как длина и ширина прямоугольника, можно найти его периметр, площадь, длину диагоналей и угол между ними. Вокруг прямоугольника всегда можно описать окружность. Эти свойства работают и в обратном направлении.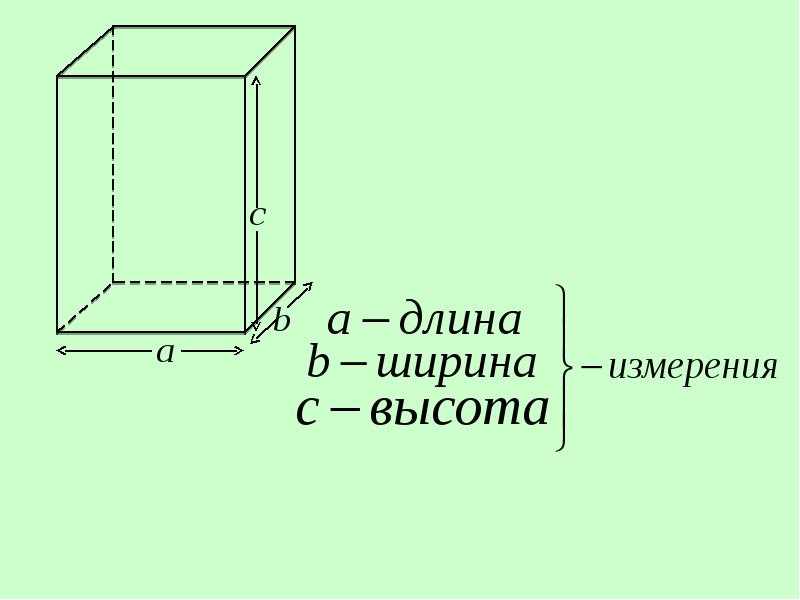 [/stop]

В чем измеряются размеры длины, ширины и высоты по СИ

По единой системе измерения длина, высота и ширина измеряются в метрах. Но иногда, если это дробное или многозначное число, для удобства в вычислениях используют кратные единицы измерения.

Для того чтобы знать, как правильно переводить единицы измерения в более крупные или же наоборот мелкие, необходимо знать значения приставок.

• Дека — 10¹,
• Гекто — 10²,
• Кило — 10³,
• Мега — 10⁶,
• Гига — 10⁹,
• Деци – 10^-1,
• Санти – 10^-2,
• Милли – 10^-3,
• Микро — 10^-6,
• Нано – 10^-9.

После подсчетов эти единицы должны быть переведены в метры.

Существуют также внесистемные единицы, но они встречаются очень редко:

• миля – 1,6 км;
• фут – 12 дюймов – 0,3048 м;
• ярд – 36 дюймов – 91,44 мм;
• дюйм – 25,4 мм и т. д.

При решении задач такие единицы должны быть переведены в метры.

При выполнении геометрических заданий единицам измерения не уделяют особого внимания, главное, чтобы они были сопоставимы

(если вы производите подсчеты в сантиметрах, значит, все величины необходимо перевести в сантиметры).

А при решении физических задач ответ должен быть дан в метрах в соответствии с единой системой измерения.

Обозначения длины, ширины, высоты в геометрии

Измеряем геометрические параметры

Вывод

Теперь вы знаете, какой буквой обозначается длина, в чем измеряется ширина прямоугольника, и сможете сами объяснить любому, как обозначаются различные параметры.

Это интересно! Легкие правила округления чисел после запятой

геометрия — Найдите идеальную ширину и высоту n одинаковых прямоугольников внутри прямоугольника

спросил
2 года 8 месяцев назад

Изменено
2 года, 8 месяцев назад

Просмотрено
132 раза

$\begingroup$

У меня есть прямоугольник, его ширина a и его высота b

Я хочу покрыть максимальную поверхность этого прямоугольника n прямоугольников, эти прямоугольники должны иметь одинаковые размеры и соблюдать соотношение w к h

как можно Я вычисляю размеры n прямоугольников?

Я пробовал следующее

$$c = \sqrt{a*b* w/h \over n}$$

$$width = c * w$$
$$height = c * h$$

Но это не совсем работает, потому что это ищет покрытие всего прямоугольника (поэтому в некоторых случаях результирующие размеры делают прямоугольник больше, чем прямоугольник ab

• геометрия
• площадь
• поверхности
• соотношение

$\endgroup$

$\begingroup$

Если на Рис.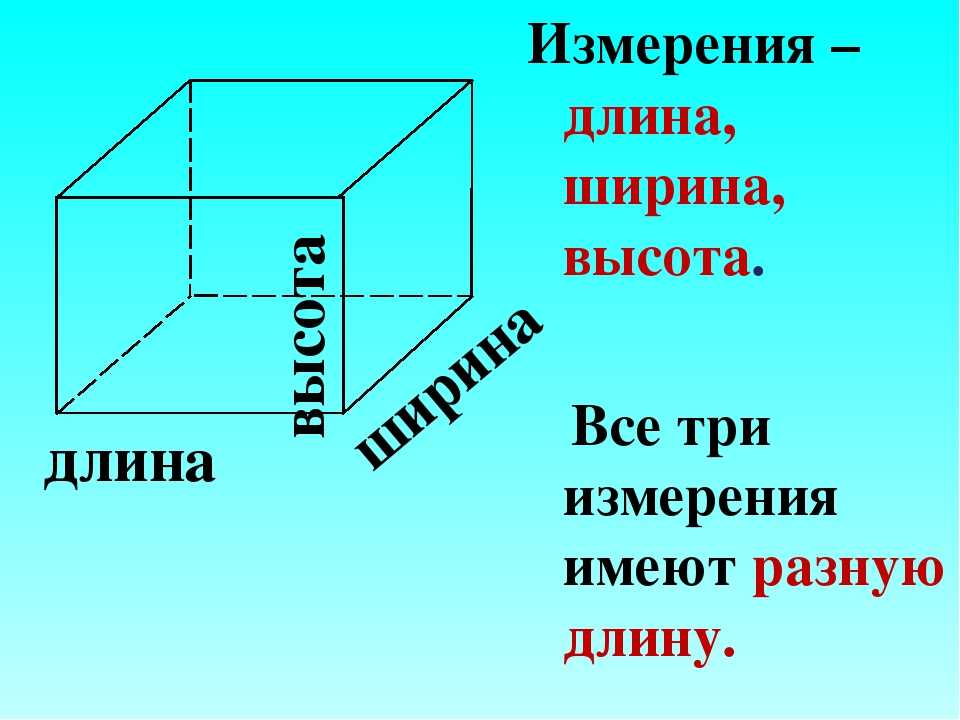 1 не показан пример того, что вы ожидаете, не читайте дальше, так как приведенное ниже описание основано на нем.

Предполагается, что заданы $a$, $b$, $h$, $w$ и $n$. Пусть высота маленьких прямоугольников равна $k$. Тогда ширина маленьких прямоугольников равна $k\frac{w}{h}$. Теперь мы можем узнать, сколько маленьких прямоугольников нам нужно, чтобы покрыть большой прямоугольник, как показано ниже

$$\mathrm{Nr.\space of\space small\space прямоугольники\space on\space a\space column} =n_c= \Big\lfloor \frac{b}{k}\Big\rfloor \le \ frac{b}{k}\qquad\quad\space$$

$$\mathrm{Nr.\space of\space small\space прямоугольники\space on\space a\space row} = n_r=\Big\lfloor \frac{a}{k} \times \frac{h}{w}\Big\rfloor \le \frac{a}{k} \times \frac{h}{w}$$

$$\следовательно \quad n = n_c\times n_r = \Big\lfloor \frac{b}{k}\Big\rfloor \times \Big\lfloor \frac{a}{k} \times \frac{h}{w}\ Большой\rэтаж \le \frac{a}{k}\times \frac{b}{k}\times \frac{h}{w}.$$

Как видите, связь между $n$ и неизвестным $k$ была получена с помощью функций пола. Эти функции не позволяют нам сделать $k$ предметом уравнения, которое нам нужно для определения высоты и ширины маленьких прямоугольников. Поэтому я думаю, что ваш вопрос не может быть решен математически. Однако можно найти решение экспериментальным путем.

$\endgroup$

6

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

геометрия — высота/ширина обрезанного круга с учетом радиуса и углов, лежащих в центре

Просто подумайте о терминах расстояния. Вам нужно найти размер наименьшего прямоугольника, который мог бы содержать ваш обрезанный диск.

Вы берете два угла $\theta_1$ и $\theta_2$. Я предполагаю, что:

$$180° \geq \theta_1 \geq \theta_2 \geq -180°$$

Вычислим $h = y_{\mathrm{max}}-y_{\mathrm{min}}$ и $w=x_{\mathrm{max}}-x_{\mathrm{min}}$, поэтому у вас есть разные возможности:

$\bullet $, если $\theta_1\geq 0 \geq \theta_2$, то $x_{ \mathrm{max}} = r$ и $x_{\mathrm{min}} = \mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\})$

$\bullet $ если $0>\theta_1 \geq \theta_2$, то $x_{\mathrm{max}} = \mathrm{max}(r \cos \theta_1, 0)$ и $x_{\mathrm{min}} = \mathrm {мин}(\{0,r \cos \theta_1,r \cos \theta_2\})$

$\bullet $ если $\theta_1 \geq \theta_2>0$, то $x_{\mathrm{max}} = \mathrm{max}(r \cos \theta_2, 0)$ и $x_{\mathrm{ min}} = \mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\})$

Мы можем суммировать это как:

$x_{\mathrm{min}} = \mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\}) $

Если $\theta_1 \theta_2 \geq 0$, то $x_{\mathrm{max}} = \mathrm {max}(\{0,r \cos \theta_1,r \cos \theta_2\})$ else $x_{\mathrm{max}} = r$

Следовательно:

$$ \boxed{w= \ влево \ {\ {начать массив} {ll}
\mathrm{max}(\{0,r \cos \theta_1,r \cos \theta_2\})-\mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\}) \ ; \mathrm{если} \; \theta_1 \theta_2 \geq 0 \\
r-\mathrm{min}(\{0,r \cos \theta_1,r \cos \theta_2\}) \text{иначе} \\
\end{массив} \right.